Count Partitions with Given Difference

Problem Statement

Given an array of integers and a target difference diff, your task is to count the number of ways to partition the array into two subsets such that the absolute difference between the sums of the subsets equals diff.

Examples

Example 1:

Input: arr = [1, 1, 2, 3], diff = 1
Output: 3

Explanation:
The subsets are
1. subset 1: [1, 2], subset 2: [1, 3], with |s1 - s2| = 1
2. subset 1: [1, 2], subset 2: [1, 3], with |s1 - s2| = 1
3. subset 1: [3], subset 2: [1, 1, 2], with |s1 - s2| = 1

Example 2:

Input: arr = [1, 2, 3, 4], diff = 3
Output: 1

Explanation:
The only valid partition is:
1. subset 1: [1, 4], subset 2: [2, 3], with |s1 - s2| = 3

Example 3:

Input: arr = [5, 2, 6, 4], diff = 3
Output: No valid partition exists.

Different Approaches

1️⃣ Recursive Approach

The original problem is to count the number of ways to partition an array into two subsets S1 and S2 such that:

• S1 - S2 = Total Difference
  • S1 + S2 = Total Difference
• S1 ≥ S2

Key Observations:

The total sum of the array (totalSum) can be used to relate S1 and S2.

Steps to form the recursive solution:

• Express the problem in terms of indexes: The array will have an index but there is one more parameter “target”. We are given the initial problem to find whether there exists in the whole array a subsequence whose sum is equal to the target.
  • So, we can say that initially, we need to find(n-1, target) which means that we are counting the number of subsequences in the array from index 0 to n-1, whose sum is equal to the target.
• Try out all possible choices at a given index: We have two choices:
  • Exclude the current element from the subsequence: We first try to find a subsequence without considering the current index element. For this, we will make a recursive call to f(ind-1, target).
  • Include the current element in the subsequence: We will try to find a subsequence by considering the current index as an element as part of the subsequence. As we have included arr[ind], the updated target which we need to find in the rest of the array will be a target - arr[ind]. Therefore, we will call f(ind-1,target-arr[ind]).

f(ind, target){
    notTaken = f(ind-1, target)
    taken = 0
    if(arr[ind] <= target)
        taken = f(ind-1, target-arr[ind])
}

Note: We will consider the current element in the subsequence only when the current element is less than or equal to the target.

• Return the sum of taken and notTaken: As we have to return the total count of subsets with the target sum, we will return the sum of taken and notTaken from our recursive call.
• Base Cases: If target == 0, it means that we have already found the subsequence from the previous steps, so we can return 1. If ind==0, it means we are at the first element, so we need to return arr[ind]==target. If the element is equal to the target we return 1 else we return 0.

Code:

#include <bits/stdc++.h>
using namespace std;

class Solution {
    const int MOD = 1e9 + 7; // Modulus value to handle large numbers and avoid overflow

public:
    /* Recursive function to count subsets with a specific target sum.
       Parameters:
       - `arr`: The input array.
       - `index`: The current index being considered.
       - `target`: The target sum to be achieved by the subset.
       Returns:
       - The number of subsets with the given target sum, modulo MOD.
    */
    int countSubsetsRecursive(vector<int>& arr, int index, int target) {
        // Step 1: If the target becomes 0, we've found a valid subset.
        if (target == 0) {
            return 1;
        }
        
        // Step 2: If the target becomes negative, no valid subset can be formed.
        if (target < 0) {
            return 0;
        }

        // Step 3: If we've processed all elements and haven't achieved the target, return 0.
        if (index >= arr.size()) {
            return 0;
        }

        // Step 4: Recursive call to include the current element in the subset.
        int includeCurrent = countSubsetsRecursive(arr, index + 1, target - arr[index]);

        // Step 5: Recursive call to exclude the current element from the subset.
        int excludeCurrent = countSubsetsRecursive(arr, index + 1, target);

        // Step 6: Combine results from both choices and take modulo MOD.
        return (includeCurrent + excludeCurrent) % MOD;
    }

    /* Function to count the number of ways to partition the array
       into two subsets with a given difference.
       Parameters:
       - `n`: Size of the array.
       - `diff`: The desired difference between the sums of the two subsets.
       - `arr`: The input array.
       Returns:
       - The number of subset pairs with the given difference.
    */
    int countPartitionsWithDifference(int n, int diff, vector<int>& arr) {
        int totalSum = 0;

        // Step 1: Calculate the total sum of all elements in the array.
        for (int num : arr) {
            totalSum += num;
        }

        // Step 2: Check if the difference condition is valid.
        // If (totalSum - diff) is negative or odd, partitioning is not possible.
        if ((totalSum - diff) < 0 || (totalSum - diff) % 2 == 1) {
            return 0;
        }

        // Step 3: Calculate the target sum for one subset.
        int targetSum = (totalSum - diff) / 2;

        // Step 4: Use the recursive function to count subsets with the target sum.
        return countSubsetsRecursive(arr, 0, targetSum);
    }
};

int main() {
    // Step 1: Input the array and difference value.
    vector<int> arr = {5, 2, 6, 4};
    int n = arr.size();
    int diff = 3;

    // Step 2: Create an instance of the Solution class.
    Solution solution;

    // Step 3: Calculate the result and print it.
    cout << "The number of subset pairs with the given difference is "
         << solution.countPartitionsWithDifference(n, diff, arr) << endl;

    return 0;
}

Complexity Analysis:

• Time Complexity: O(2^N), As there are 2 choices for each index.
• Space Complexity: O(N), As we are using recursion stack of depth N.

2️⃣ Memoization

If we draw the recursion tree, we will see that there are overlapping subproblems. Hence the DP approaches can be applied to the recursive solution.

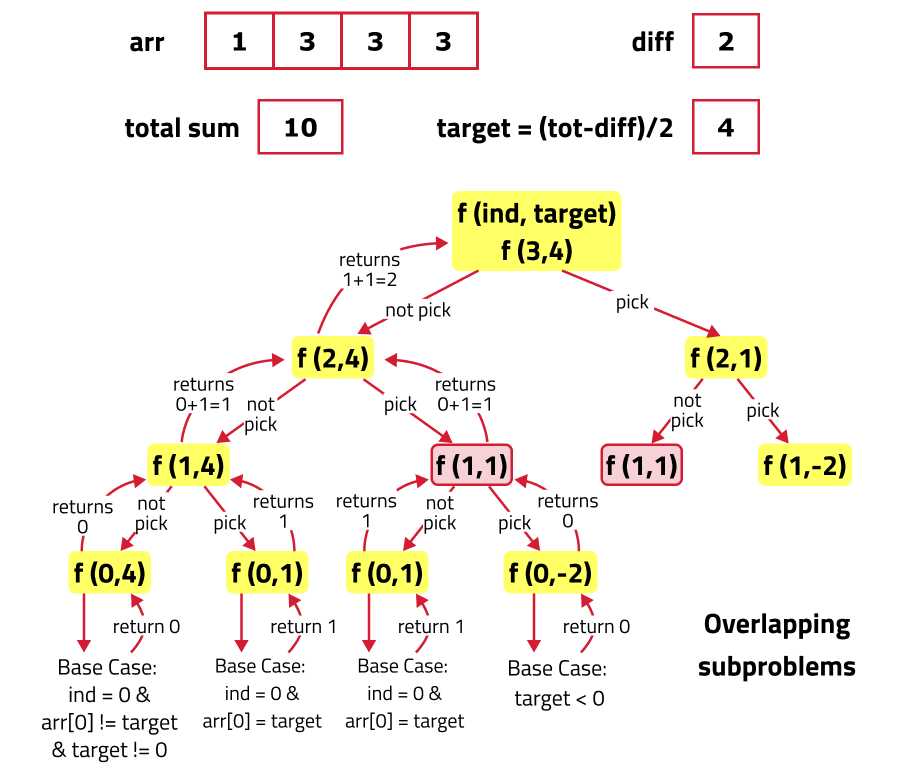
In order to convert a recursive solution to memoization the following steps will be taken:

• Declare a dp array of size [n][k+1]: As there are two changing parameters in the recursive solution, 'ind' and 'k'. The maximum value 'ind' can attain is (n-1){0 to n-1}, where n is the size of array and for 'k' only values from 0 to k is possible. Therefore, we need 2D dp array.
  • The dp array stores the calculations of subproblems. Initialize dp array with -1, to indicate that no subproblem has been solved yet.
• While encountering an overlapping subproblem: When we come across a subproblem, for which the dp array has value other than -1, it means we have found a subproblem which has been solved before hence it is an overlapping subproblem. No need to calculate it's value again just retrieve the value from dp array and return it.
• Store the value of subproblem: Whenever, a subproblem is encountered and it is not solved yet(the value at this index will be -1 in the dp array), store the calculated value of subproblem in the array.

Code:

#include <bits/stdc++.h>
using namespace std;

class Solution {
    const int MOD = 1e9 + 7; // Modulus value to handle large numbers and avoid overflow

public:
    /* Recursive function with memoization to count subsets with a specific target sum.
       Parameters:
       - `arr`: The input array.
       - `index`: The current index being considered.
       - `target`: The target sum to be achieved by the subset.
       - `dp`: The memoization table to store results of subproblems.
       Returns:
       - The number of subsets with the given target sum, modulo MOD.
    */
    int countSubsetsRecursive(vector<int>& arr, int index, int target, vector<vector<int>>& dp) {
        // Base Case 1: If the target becomes 0, we've found a valid subset.
        if (target == 0) {
            return 1;
        }

        // Base Case 2: If we've processed all elements or target becomes invalid.
        if (index >= arr.size() || target < 0) {
            return 0;
        }

        // Check if the result is already computed.
        if (dp[index][target] != -1) {
            return dp[index][target];
        }

        // Recursive Case 1: Include the current element in the subset.
        int includeCurrent = countSubsetsRecursive(arr, index + 1, target - arr[index], dp);

        // Recursive Case 2: Exclude the current element from the subset.
        int excludeCurrent = countSubsetsRecursive(arr, index + 1, target, dp);

        // Store the result in the dp table and return it modulo MOD.
        return dp[index][target] = (includeCurrent + excludeCurrent) % MOD;
    }

    /* Function to count the number of ways to partition the array
       into two subsets with a given difference.
       Parameters:
       - `n`: Size of the array.
       - `diff`: The desired difference between the sums of the two subsets.
       - `arr`: The input array.
       Returns:
       - The number of subset pairs with the given difference.
    */
    int countPartitions(int n, int diff, vector<int>& arr) {
        int totalSum = 0;

        // Step 1: Calculate the total sum of all elements in the array.
        for (int num : arr) {
            totalSum += num;
        }

        // Step 2: Check if the difference condition is valid.
        // If (totalSum - diff) is negative or odd, partitioning is not possible.
        if ((totalSum - diff) < 0 || (totalSum - diff) % 2 == 1) {
            return 0;
        }

        // Step 3: Calculate the target sum for one subset.
        int targetSum = (totalSum - diff) / 2;

        // Step 4: Initialize the dp table for memoization.
        vector<vector<int>> dp(n, vector<int>(targetSum + 1, -1));

        // Step 5: Use the recursive function to count subsets with the target sum.
        return countSubsetsRecursive(arr, 0, targetSum, dp);
    }
};

int main() {
    // Input the array and difference value.
    vector<int> arr = {5, 2, 6, 4};
    int n = arr.size();
    int diff = 3;

    // Create an instance of the Solution class.
    Solution solution;

    // Calculate the result and print it.
    cout << "The number of subset pairs with the given difference is "
         << solution.countPartitions(n, diff, arr) << endl;

    return 0;
}

Complexity Analysis:

• Time Complexity:
  • Pre Computation:
    • Calculating the total sum of the array takes O(n).
  • The recursive function solves the problem using a top-down dynamic programming approach with memoization.
    • The recursion processes states defined by the two parameters:
      • index = ranges from 0 to n - 1, where n is the size of the array.
      • target = ranges from 0 to targetSum,
    • The memoization table dp[index][target] ensures that each state (index, target) is computed only once.
    • Thus number of unique states is:
      • n * (targetSum + 1)
      • Each state is computed in O(1) time.
  • Overall Time Complexity:
    • O(n * targetSum) + O(n) ~ O(n * targetSum)
      • where targetSum = (totalSum - diff) / 2
• Space Complexity:
  • The dp table has dimensions n * (targetSum + 1), so it consumes:
    • O(n * targetSum)
  • The recursion depth is at most n
  • Overall Space Complexity:
    • O(n * targetSum) + O(n)