Problem Statement

Given a weighted undirected graph having n vertices numbered from 1 to n and m edges describing there are edges, where edges[i] = [ai, bj, wi], representing an edge from vertex ai to bj with weight wi.

Find the shortest path between the vertex 1 and the vertex n and if path does not exist then return a list consisting of only -1. If there exists a path, then return a list whose first element is the weight of the path and the remaining represents the shortest path from vertex 1 to vertex n.

Examples

Example 1:

Input: n = 5, m = 6,
       edges = [
                [1, 2, 2],
                [2, 5, 5],
                [2, 3, 4],
                [1, 4, 1],
                [4, 3, 3],
                [3, 5, 1]
               ]
Output: 5 1 4 3 5

Explanation: The source vertex is 1. Hence, the shortest distance path of node 5 from the source will be 1->4->3->5 as this is the path with a minimum sum of edge weights from source to destination.

Example 2:

Input: n = 4, m = 4,
       edges = [
                [1, 2, 2],
                [2, 3, 4],
                [1, 4, 1].
                [4, 3, 3]
               ]
Output: 1 4

Explanation: The source vertex is 1. Hence, the shortest distance path of node 4 from the source will be 1->4 as this is the path with the minimum sum of edge weights from source to destination.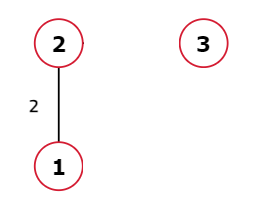

Example 3:

Input: n = 3, m = 1,
       edges = [
                [1, 2, 2]
               ]
Output: -1

Explanation: As there is no path from the source 1 to destination 3, so return -1.

Different Approaches

1️⃣ Dijkstra Algorithm

Intuition:

Since the problem requires the shortest path from source node(node 1) to node n, the first thought that must come to the mind is to use Dijkstra's Algorithm.

Modification:

Since the shortest path needs from source node(node 1) to node n is required, for every node possible, its parent node must be stored via which the node is reachable through minimum distance. Hence, in the Dijkstra's Algorithm, a slight modification can be done where whenever an edge relaxation happens for a particular node, it's parent node is stored in an array.

Approach:

1. Use a priority queue to process nodes by their shortest known distance.
2. Initialize two array
   1. One to store shortest distances, with the source node set to 0 and all others to infinity.
   2. Another for parent nodes, setting each node as its own parent initially.
3. Add the source node to the priority queue with a distance of 0.
4. Extract the node with the smallest distance from the queue and perfom edge relaxation (update the distances to its neighbors if a shorter path is found). Add the updated neighbors back to the queue and update the parent of node.
5. The distance array maintains the shortest distances from the source to all nodes, while the parent array tracks the path.
6. If the destination node is reachable, use the parent array to trace back from the destination to the source, forming the path. If unreachable, return [-1].

Code:

#include <bits/stdc++.h>
using namespace std;

/* Define P as a shorthand 
for the pair<int, int> type */
#define P pair<int,int>

class Solution {
public:
    /* Function to find the shortest 
    path from node 1 to node n */
    vector<int> shortestPath(int n, int m, 
                vector<vector<int>> &edges) {
                    
        // Adjacency list to store graph
        vector<pair<int, int>> adj[n + 1];
        
        // Adding the edges to the graph
        for (auto it : edges) {
            adj[it[0]].push_back({it[1], it[2]});
            adj[it[1]].push_back({it[0], it[2]});
        }
        
        
        /* Using priority queue to 
        implement Dijkstra Algorithm */
        priority_queue<P, vector<P>, greater<P>> pq;

        // Distance array
        vector<int> dist(n + 1, 1e9);
        
        // Parent array
        vector<int> parent(n + 1);
        
        /* Marking each node as 
        its own parent initially */
        for (int i = 1; i <= n; i++)
            parent[i] = i;
        
        /* Distance of source node 
        (node 1) to itself is zero */
        dist[1] = 0;

        // Push the source node to the queue.
        pq.push({0, 1});
        
        // Until the queue is empty
        while (!pq.empty())
        {
            /* Get the pair containing node having 
            minimum distance from source node */
            auto it = pq.top();
            pq.pop();
            
            int node = it.second; // node
            int dis = it.first; // distance

            // Iterate through the neighbors
            for (auto it : adj[node]) {
                
                int adjNode = it.first; // node
                int edWt = it.second; // edge weight

                /* If the tentative distance to 
                reach adjacent node is smaller 
                than the known distance */
                if (dis + edWt < dist[adjNode]) {
                    
                    // Update the known distance
                    dist[adjNode] = dis + edWt;
                    
                    // Push the new pair to priority queue
                    pq.push({dis + edWt, adjNode});

                    /* Update the parent of the adjNode 
                    to the recent node(where it came from) */
                    parent[adjNode] = node;
                }
            }
        }

        /* If distance to the node could not be found, 
        return an array containing -1. */
        if (dist[n] == 1e9)
            return {-1};

        // Array to store the path
        vector<int> path;
        
        // Start from the destination node
        int node = n;
        
        /* Iterate backwards from destination 
        to source through the parent array */
        while (parent[node] != node) {
            
            // Add the node to the path
            path.push_back(node); 
            
            // Take a step back
            node = parent[node];
        }
        
        // Add the source node to the path
        path.push_back(1);

        /* Since the path stored is in a 
        reverse order, reverse the array 
        to get the actual path */
        reverse(path.begin(), path.end());
        
        // Add the path weight in the beginning
        path.insert(path.begin(), dist[n]);
        
        // Return the result
        return path;
    }
};

int main() {
    
    int n = 5, m = 6;
    vector<vector<int>> edges = {
        {1,2,2}, {2,5,5}, {2,3,4}, 
        {1,4,1}, {4,3,3}, {3,5,1}
    };
    
    /* Creating an instance of 
    Solution class */
    Solution sol; 
    
    /* Function call to find the shortest distance 
    of each node from the source node */
    vector<int> ans = sol.shortestPath(n, m, edges);
    
    // Output
    cout << "The resulting path weight is: " << ans[0] << endl;
    cout << "The path is: " << endl;
    for(int i=1; i < ans.size(); i++) {
        cout << ans[i] << " ";
    }
    
    return 0;
}

Complexity Analysis:

• Time Complexity: O((N+M)*logN)
  • Each node is processed once in the priority queue and deletion and insertion operation takes O(logN) time making it overall O(N*logN) in the worst case.
  • For each vertex, all its edges are relaxed. This operation involves updating the priority queue, which takes O(logV) making it overall O(M*logN) for E edges in the worst case.
  • Reconstructing the path involves tracing the parent array, which takes O(N) in the worst case (since we may trace back through all vertices).
• Space Complexity: O(N)
  • The priority queue will store distances to all nodes in worst case leading to O(N) space.
  • The distance array and parent array takes O(N) space each.
  • The path array will store O(N) nodes in the worst case.