Problem Statement
You are given a 2D grid representing a map of '1's (land) and '0's (water). An island is a group of adjacent lands connected horizontally or vertically (including diagonally). The grid is surrounded by water, and each cell is either '1' or '0'. Your task is to determine the number of islands on the map.
Input:
- A 2D binary grid (
grid[i][j]), where:'1'represents land.'0'represents water.
Output:
- The number of distinct islands where islands are connected not only vertically and horizontally but also diagonally.
Examples
Example 1:
Input: grid = [
['1', '1', '1', '0', '0'],
['1', '1', '0', '0', '0'],
['1', '1', '0', '0', '1'],
['0', '0', '0', '1', '1']
]
Output: 2
Explanation:
0 1 2 3 4
+-----+-----+-----+-----+-----+
0 | 1 | 1 | 1 | 0 | 0 |
+-----+-----+-----+-----+-----+
1 | 1 | 1 | 0 | 0 | 0 |
+-----+-----+-----+-----+-----+
2 | 1 | 1 | 0 | 0 | 1 |
+-----+-----+-----+-----+-----+
3 | 0 | 0 | 0 | 1 | 1 |
+-----+-----+-----+-----+-----+
It has two islands,
one formed by - [
(0, 0),
(0, 1),
(0, 2),
(1, 0),
(1, 1),
(2, 0),
(2, 1)
]
second is formed by -
[
(2, 4),
(3, 3),
(3, 4)
]
0 1 2 3 4
+-----+-----+-----+
0 | 1 | 1 | 1 |
+-----+-----+-----+
1 | 1 | 1 |
+-----+-----+ +-----+
2 | 1 | 1 | | 1 |
+-----+-----+ +-----+-----+
3 | 1 | 1 |
+-----+-----+Example 2:
Input: grid = [
['1', '1', '1', '0', '1'],
['1', '1', '0', '0', '0'],
['1', '1', '0', '0', '1'],
['0', '0', '1', '1', '1']
]
Output: 2
Explanation:
0 1 2 3 4
+-----+-----+-----+-----+-----+
0 | 1 | 1 | 1 | 0 | 1 |
+-----+-----+-----+-----+-----+
1 | 1 | 1 | 0 | 0 | 0 |
+-----+-----+-----+-----+-----+
2 | 1 | 1 | 0 | 0 | 1 |
+-----+-----+-----+-----+-----+
3 | 0 | 0 | 1 | 1 | 1 |
+-----+-----+-----+-----+-----+
It has two islands,
one formed by - [
(0, 0),
(0, 1),
(0, 2),
(1, 0),
(1, 1),
(2, 0),
(2, 1),
(2, 4),
(3, 2),
(3, 3),
(3, 4)
]
second is formed by -
[
(0, 4),
]
0 1 2 3 4
+-----+-----+-----+ +-----+
0 | 1 | 1 | 1 | | 1 |
+-----+-----+-----+ +-----+
1 | 1 | 1 |
+-----+-----+ +-----+
2 | 1 | 1 | | 1 |
+-----+-----+-----+-----+-----+
3 | 1 | 1 | 1 |
+-----+-----+-----+Different Approaches
1️⃣ BFS
Intuition:
How to solve this problem using a graph?
- Think of all the cells in the grid as nodes or vertices which are connected through each other via 8 edges.
How to traverse the neighbors efficiently?
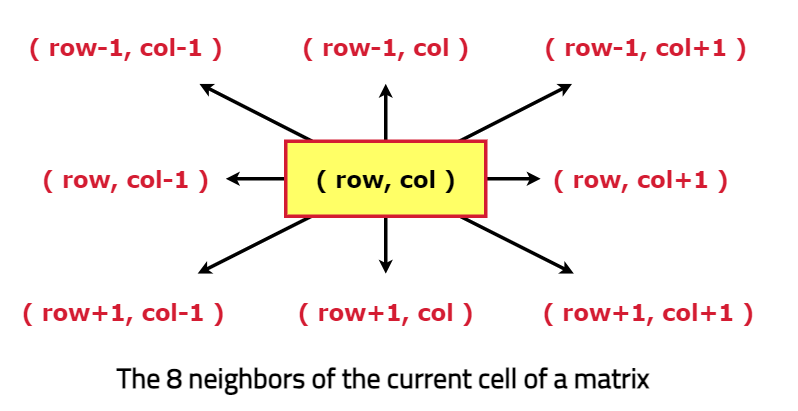
The 8 neighbors of the current cell can be shown like this:
+-----------------------+-----------------------+-----------------------+
| (row - 1, column - 1) | (row - 1, column) | (row - 1, column + 1) |
+-----------------------+-----------------------+-----------------------+
| (row, column - 1) | (row, column) | (row, column + 1) |
+-----------------------+-----------------------+-----------------------+
| (row + 1, column - 1) | (row + 1, column) | (row, column + 1) |
+-----------------------+-----------------------+-----------------------+It is clear from the above illustration that:
rowcan berow-1,row,row+1. Such that it varies from-1 to 1.colcan becol-1,col,col+1. Such that it varies from-1 to 1.
Therefore, to effectively traverse all the neighbors, two loops can be used.
Approach:
- Determine the dimensions of grid. Create a 2D visited array and initialize all values as false. Initialize a counter for the number of islands.
- Loop through each cell in the grid. If the cell is land and not yet visited, it signifies the start of a new island.
- Use BFS to explore all connected land cells starting from this cell and mark them visited. Increase the island count after completing the BFS for the current island.
Code:
#include <bits/stdc++.h>
using namespace std;
class Solution {
private:
/* Function to determine if the cell
is valid (within grid's boundaries) */
bool isValid(int i, int j, int n, int m) {
if (i < 0 || i >= n) return false;
if (j < 0 || j >= m) return false;
// Return true if cell is valid
return true;
}
void bfs(int i, int j, vector<vector<bool>>& vis,
vector<vector<char>>& grid) {
// Mark the node as visited
vis[i][j] = true;
// Queue required for BFS traversal
queue<pair<int, int>> q;
// push the node in queue
q.push({i, j});
// Dimensions of grid
int n = grid.size();
int m = grid[0].size();
// Until the queue becomes empty
while (!q.empty()) {
// Get the cell from queue
pair<int, int> cell = q.front();
q.pop();
// Determine its row & column
int row = cell.first;
int col = cell.second;
// Traverse the 8 neighbours
for (int delRow = -1; delRow <= 1; delRow++) {
for (int delCol = -1; delCol <= 1; delCol++) {
// Coordinates of new cell
int newRow = row + delRow;
int newCol = col + delCol;
/* Check if the new cell is valid,
unvisited, and a land cell */
if (isValid(newRow, newCol, n, m)
&& grid[newRow][newCol] == '1'
&& !vis[newRow][newCol]) {
// Mark the node as visited
vis[newRow][newCol] = true;
// Push new cell in queue
q.push({newRow, newCol});
}
}
}
}
}
public:
// Function to find the number of islands in given grid
int numIslands(vector<vector<char>>& grid) {
// Size of the grid
int n = grid.size();
int m = grid[0].size();
// Visited array
vector<vector<bool>> vis(n, vector<bool>(m, false));
// To store the count of islands
int count = 0;
// Traverse the grid
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
/* If not visited and is a land,
start a new traversal */
if (!vis[i][j] && grid[i][j] == '1') {
count++;
bfs(i, j, vis, grid);
}
}
}
return count;
}
};
int main() {
vector<vector<char>> grid = {
{'1', '1', '1', '0', '1'},
{'1', '0', '0', '0', '0'},
{'1', '1', '1', '0', '1'},
{'0', '0', '0', '1', '1'}
};
// Creating an instance of Solution class
Solution sol;
/* Function call to find the
number of islands in given grid */
int ans = sol.numIslands(grid);
cout << "The total islands in given grids are: " << ans << endl;
return 0;
}
Complexity Analysis:
- Time Complexity:
O(N*M)(where N and M are the dimensions of the grid)- Running a nested loop to traverse every cell of grid takes
O(N*M)time. - In total, the traversal will be performed on grids taking overall at most of
O(9*N*M)time.
- Running a nested loop to traverse every cell of grid takes
- Space Complexity:
O(N*M)- Because of the visited array, it takes up
O(N*M)space and the queue space will also beO(N*M)at most.
- Because of the visited array, it takes up
2️⃣ DFS
We can solve it using the DFS as well.
Code:
class Solution{
public:
// Function to check if a cell is within the grid bounds.
bool valid(int row, int col, int n, int m) {
// Check if the row index is out of bounds.
if(row < 0 || row >= n) {
return false;
}
// Check if the column index is out of bounds.
if(col < 0 || col >= m) {
return false;
}
// The cell is within bounds.
return true;
}
// Recursive function to perform DFS and mark all connected land cells as visited.
void recursive(int row, int col, vector<vector<char>>& grid, vector<vector<int>>& vis, int n, int m){
// Mark the current cell as visited.
vis[row][col] = 1;
// Traverse all 8 neighbors (including diagonals).
for(int dx = -1; dx <= 1; dx++) {
for(int dy = -1; dy <= 1; dy++) {
int posX = row + dx; // Calculate neighbor's row index.
int posY = col + dy; // Calculate neighbor's column index.
// Check if the neighbor is within bounds, is part of an island ('1'),
// and has not been visited yet.
if (valid(posX, posY, n, m) && grid[posX][posY] == '1' && !vis[posX][posY]){
// Recursively visit the neighbor.
recursive(posX, posY, grid, vis, n, m);
}
}
}
}
// Function to count the number of islands in the grid.
int numIslands(vector<vector<char>> &grid){
int n = grid.size(); // Number of rows in the grid.
int m = grid[0].size(); // Number of columns in the grid.
// Create a visited matrix initialized to 0 (false) for all cells.
vector<vector<int>> vis(n, vector<int>(m, 0));
int count = 0; // Initialize island count.
// Iterate over every cell in the grid.
for(int row = 0; row < n; row++) {
for (int col = 0; col < m; col++) {
// Skip water cells.
if(grid[row][col] == '0'){
continue;
}
// If the cell is land and not visited, it is part of a new island.
if(!vis[row][col]){
count++; // Increment island count.
// Start a DFS from this cell to mark all connected land cells.
recursive(row, col, grid, vis, n, m);
}
}
}
// Return the total number of islands found.
return count;
}
};
