Problem Statement

Given an array arr of size n, where each element arr[i] represents the stock price on day i. Calculate the span of stock prices for each day.

The span Si for a specific day i is defined as the maximum number of consecutive previous days (including the current day) for which the stock price was less than or equal to the price on day i.

Examples

Example 1:

Input: n = 7, arr = [120, 100, 60, 80, 90, 110, 115]
Output: 1 1 1 2 3 5 6

Explanation:
Traversing the given input span:
120 is greater than or equal to 120 and there are no more elements behind it so the span is 1,
100 is greater than or equal to 100 and smaller than 120 so the span is 1,
60 is greater than or equal to 60 and smaller than 100 so the span is 1,
80 is greater than or equal to 60, 80 and smaller than 100 so the span is 2,
90 is greater than or equal to 60, 80, 90 and smaller than 100 so the span is 3,
110 is greater than or equal to 60, 80, 90, 100, 110 and smaller than 120 so the span is 5,
115 is greater than or equal to all previous elements and smaller than 120 so the span is 6.
Hence the output will be 1 1 1 2 3 5 6.

Input: n = 6, arr = [15, 13, 12, 14, 16, 20]
Output: 1 1 1 3 5 6

Explanation:
Traversing the given input span:
15 is greater than or equal to 15 and there are no more elements behind it so the span is 1,
13 is greater than or equal to 13 and smaller than 15 so the span is 1,
12 is greater than or equal to 12 and smaller than 13 so the span is 1,
14 is greater than or equal to 12, 14 and smaller than 15 so the span is 2,
16 is greater than or equal to 12, 14, 15, 16 and smaller than 20 so the span is 4,
20 is greater than or equal to all previous elements so the span is 6.
Hence the output will be 1 1 1 2 4 6.

Different Approaches

1️⃣ Brute Force Approach

Intuition:

The brute force to solve the problem is to start counting the days (for each day) where the stock prices were less than or equal to the price of stocks on current day.

Approach:

1. Initialize an array to store the answer. Start traversing on the given array.
2. For every element, traverse back till the stock prices are less than or equal to the stock prices on current day.
3. Store the stock span for each day. Once done, return the answer.

Code:

#include <bits/stdc++.h>
using namespace std;

class Solution {
public:
    // Function to find the span of stock prices for each day
    vector <int> stockSpan(vector<int> arr, int n) {
        
        // To store the answer
        vector<int> ans(n);
        
        // Traverse on the array
        for(int i=0; i < n; i++) {
            
            // To store the current span of stocks
            int currSpan = 0;
            
            // Traversing backwards to find stock span
            for(int j=i; j >= 0; j--) {
            
                // Update stock span
                if(arr[j] <= arr[i]) {
                    currSpan++;
                }
                
                // Else break out from loop
                else break;
            }
            
            // Store the current span
            ans[i] = currSpan;
        }
        
        // Return the result
        return ans;
    }
};

int main() {
    int n = 7;
    vector<int> arr = {120, 100, 60, 80, 90, 110, 115};
    
    /* Creating an instance of 
    Solution class */
    Solution sol; 
    
    /* Function call to find the span 
    of stock prices for each day */
    vector<int> ans = sol.stockSpan(arr, n);
    
    cout << "The span of stock prices is: ";
    for(int i=0; i < n; i++) {
        cout << ans[i] << " ";
    }
    
    return 0;
}

Complexity Analysis:

• Time Complexity:O(N^2) (where N is the length of given array)
  • Using two nested loops.
• Space Complexity:O(1)
  • Using only a couple of variables.

2️⃣ Optimal Approach

Intuition:

As stated in the problem, the stock span is the number of consecutive days for which the stock price was less than or equal to the price on current day. Hence, to get the stock span for current day, the aim is to find the position of its previous greater element. This will significantly improve the solution by eliminating multiple backwards traversals on the given array.

Understanding:

Finding the previous greater element is similar to finding the next greater element, the only difference is that the direction of traversal will be reversed while maintaining the decreasing order of elements in the stack (monotonic stack).

Approach:

1. Determine the indices of previous greater elements using monotonic stack (maintaining elements in decreasing order in a stack)
2. Once the indices are known, the stock span for each day will be difference between the current index and the index of its previous greater element.
3. Traverse the array, updating the stock span for each day.
4. After the traversal is over, return the result.

Dry Run:

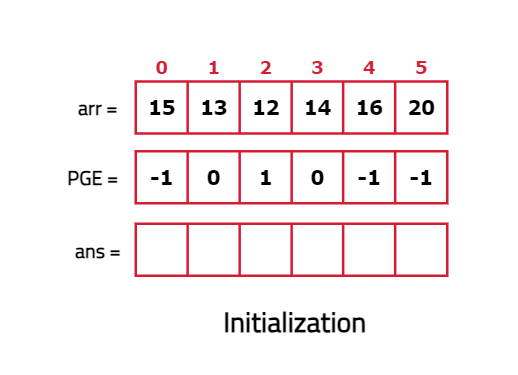
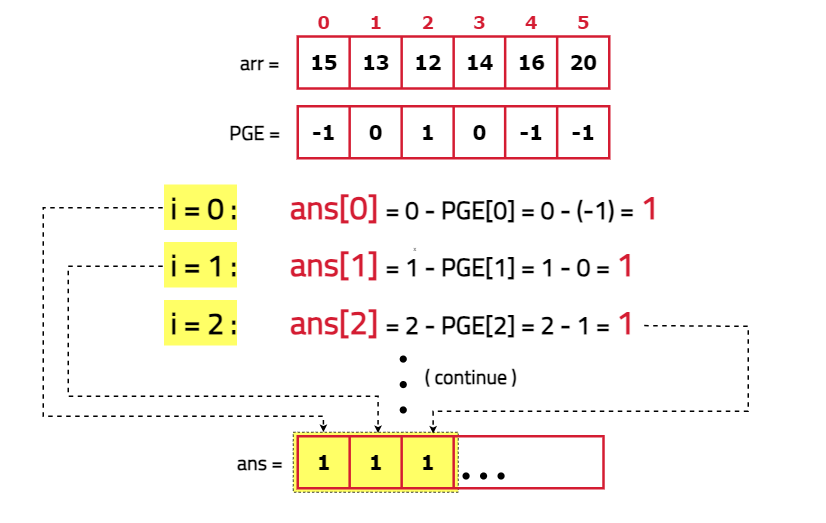
Code:

#include <bits/stdc++.h>
using namespace std;

class Solution {
private:
    /* Function to find the indices of previous 
    greater element for each element in the array */
    vector<int> findPGE(vector<int> arr) {
        
        int n = arr.size(); //size of array
        
        // To store the previous greater elements
        vector<int> ans(n);
        
        // Stack to get elements in LIFO fashion
        stack<int> st;
        
        // Start traversing from the front
        for(int i=0; i < n; i++) {
            
            // Get the current element
            int currEle = arr[i];
            
            /* Pop the elements in the stack until 
            the stack is not empty and the top 
            element is not the greater element */
            while(!st.empty() && arr[st.top()] <= currEle) {
                st.pop();
            }
            
            /* If the greater element is not 
            found, stack will be empty */
            if(st.empty()) 
                ans[i] = -1;
                
            // Else store the answer
            else 
                ans[i] = st.top();
            
            // Push the current index in the stack 
            st.push(i);
        }
        
        // Return the result
        return ans;
    }
    
public:
    // Function to find the span of stock prices for each day
    vector <int> stockSpan(vector<int> arr, int n) {
        
        // Get the indices of previous greater elements
        vector<int> PGE = findPGE(arr);
        
        
        // To store the answer
        vector<int> ans(n);
        
        // Compute the result
        for(int i=0; i < n; i++) {
            ans[i] = i - PGE[i];
        }
        
        // Return the result
        return ans;
    }
};

int main() {
    int n = 7;
    vector<int> arr = {120, 100, 60, 80, 90, 110, 115};
    
    /* Creating an instance of 
    Solution class */
    Solution sol; 
    
    /* Function call to find the span 
    of stock prices for each day */
    vector<int> ans = sol.stockSpan(arr, n);
    
    cout << "The span of stock prices is: ";
    for(int i=0; i < n; i++) {
        cout << ans[i] << " ";
    }
    
    return 0;
}

Complexity Analysis:

• Time Complexity:O(N)
  • Finding the indices of previous greater elements takes O(N) time.
  • Traversing the array once to find the stock span taking O(N) time.
• Space Complexity:O(N)
  • The stack space used to find the previous greater elements can go up to O(N) in the worst case.