Problem Statement

The Tower of Hanoi is a classic mathematical puzzle that involves three rods and a number of disks of different sizes. The puzzle starts with all the disks stacked in ascending order of size on the first rod (the largest disk at the bottom and the smallest at the top).

The objective of the puzzle is to move the entire stack of disks from the first rod to the third rod, following these rules:

1. Only one disk can be moved at a time.
2. Each move involves taking the top disk from one of the rods and placing it on top of another rod.
3. A larger disk cannot be placed on top of a smaller disk.

Problem Input

• Number of disks (n): The total number of disks to be moved.

Problem Output

• A sequence of moves required to transfer all the disks from the first rod to the third rod, while obeying the rules.

Examples

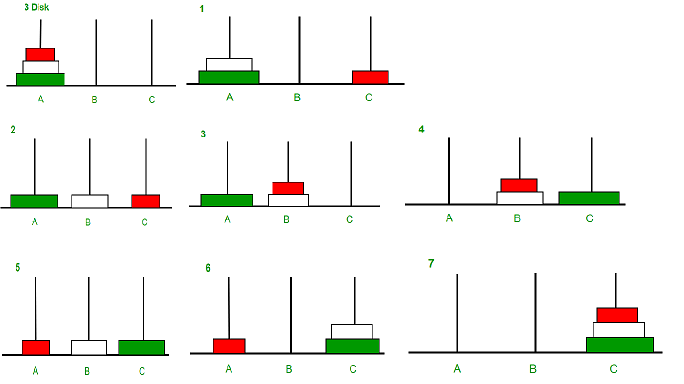
Input: n = 3 (3 disks)

Output:

Move disk 1 from rod A to rod C
Move disk 2 from rod A to rod B
Move disk 1 from rod C to rod B
Move disk 3 from rod A to rod C
Move disk 1 from rod B to rod A
Move disk 2 from rod B to rod C
Move disk 1 from rod A to rod C

The minimum number of moves required to solve the puzzle with n disks is 2^n - 1.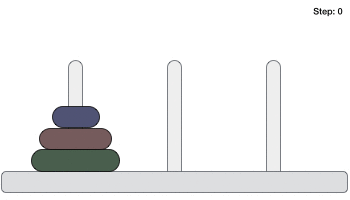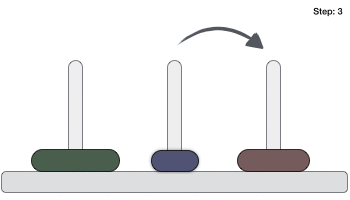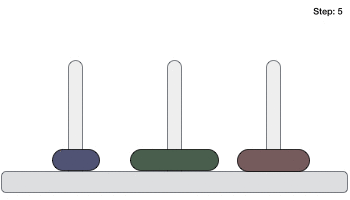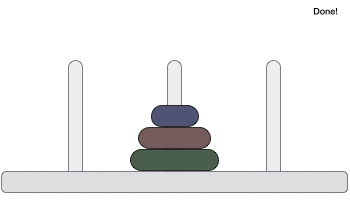

Different Approaches

1️⃣ Recursion:

Intuition Behind the Tower of Hanoi

The Tower of Hanoi problem is fundamentally about breaking down a complex problem into simpler, more manageable subproblems using recursion. Our goal is to move n disks from the source rod (say, A) to the destination rod (say, C) using an auxiliary rod (say, B) while obeying the problem's rules.

To do this efficiently, we need to recognize a pattern:

• If we know how to move n-1 disks, we can solve the problem for n disks using a few strategic moves:
  1. Move the top n-1 disks from the source rod to the auxiliary rod.
  2. Move the largest disk (the n-th disk) from the source rod to the destination rod.
  3. Finally, move the n-1 disks from the auxiliary rod to the destination rod.

Approach Using the IBH (Induction, Base Case, Hypothesis) Method

The IBH method is a structured way to understand recursion:

1. Induction (Recursive Approach):
   • We assume that the problem can be solved recursively for n-1 disks, which is our "hypothesis."
   • Our goal is to use this hypothesis to solve the problem for n disks.
2. Base Case:
   • When n = 1, the problem is trivial: We only need to move one disk from the source rod to the destination rod. This is our base case.
3. Hypothesis:
   • Assume that we know how to move n-1 disks from the source rod to the auxiliary rod. This assumption helps us proceed with solving the problem for n disks.

Step-by-Step Approach Using IBH Method

1. Base Case: If there is only one disk (n = 1), simply move the disk from the source rod to the destination rod.
2. Hypothesis: Assume you can solve the problem for n-1 disks. This means you can move n-1 disks from the source rod to the auxiliary rod, and then from the auxiliary rod to the destination rod.
3. Induction (Recursive Steps):
   • To move n disks from the source rod to the destination rod:
     1. Move the top n-1 disks from the source rod to the auxiliary rod using the destination rod as an auxiliary.
     2. Move the nth (largest) disk from the source rod to the destination rod.
     3. Move the n-1 disks from the auxiliary rod to the destination rod using the source rod as an auxiliary.

Code:

#include <iostream>
using namespace std;

void towerOfHanoi(int n, char source, char destination, char auxiliary) {
    // Base Case: If there's only one disk, move it directly
    if (n == 1) {
        cout << "Move disk 1 from " << source << " to " << destination << endl;
        return;
    }
    
    // Step 1: Move n-1 disks from source to auxiliary using destination as helper
    towerOfHanoi(n - 1, source, auxiliary, destination);

    // Step 2: Move the nth disk from source to destination
    cout << "Move disk " << n << " from " << source << " to " << destination << endl;

    // Step 3: Move n-1 disks from auxiliary to destination using source as helper
    towerOfHanoi(n - 1, auxiliary, destination, source);
}

int main() {
    int n;
    cout << "Enter the number of disks: ";
    cin >> n;
    towerOfHanoi(n, 'A', 'C', 'B'); // A: Source, C: Destination, B: Auxiliary
    return 0;
}