Problem Statement
Given an m x n matrix mat of integers, sort each of the diagonals in the matrix in ascending order. A diagonal in the matrix is defined as all elements that have the same difference between their row and column indices. Return the matrix with all diagonals sorted.
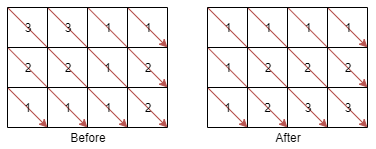
Examples
Example 1:
Input:
mat = [
[3, 3, 1, 1],
[2, 2, 1, 2],
[1, 1, 1, 2]
]
Output:
[
[1, 1, 1, 1],
[2, 2, 2, 2],
[3, 3, 3, 2]
]
Different Approaches
1️⃣ Hash Map Based Sorting
Intuition:
Each diagonal can be thought of as an independent sub-array. For example, for any element at mat[i][j], all elements on the same diagonal will have the same difference i - j. Therefore, we can treat these diagonals separately, sort the elements within each diagonal, and then place them back in their respective positions in the matrix.
Key Idea:
- Group elements based on the diagonal they belong to. Since all elements on the same diagonal have the same value for
i - j, we can use this as the key. - Extract all the elements for each diagonal, sort them, and then place the sorted elements back into the matrix.
Approach: Hash Map Based Sorting
- Group Elements by Diagonal:
- Use a hash map (or dictionary) where the key is
i - jand the value is a list of all elements belonging to that diagonal.
- Use a hash map (or dictionary) where the key is
- Sort Each Diagonal:
- Sort each list of elements corresponding to a diagonal in ascending order.
- Place the Sorted Elements Back:
- Traverse the matrix again and place the sorted elements back into their original diagonal positions.
Dry Run:
Initialization:
+------+------+------+------+
mat = | 3 | 3 | 1 | 1 |
+------+------+------+------+
[0, 0] [0, 1] [0, 2] [0, 3]
+------+------+------+------+
| 2 | 2 | 1 | 2 |
+------+------+------+------+
[1, 0] [1, 1] [1, 2] [1, 3]
+------+------+------+------+
| 1 | 1 | 1 | 2 |
+------+------+------+------+
[2, 0] [2, 1] [2, 2] [2, 3]
map = key->(i-j), value-> vectorStep 1: Push elements into the corresponding diagonal in the map.
+------+------+------+------+
mat = | 3 | 3 | 1 | 1 |
+------+------+------+------+
[0, 0] [0, 1] [0, 2] [0, 3]
+------+------+------+------+
| 2 | 2 | 1 | 2 |
+------+------+------+------+
[1, 0] [1, 1] [1, 2] [1, 3]
+------+------+------+------+
| 1 | 1 | 1 | 2 |
+------+------+------+------+
[2, 0] [2, 1] [2, 2] [2, 3]
map = key->(i-j), value-> vector
Loop through the matrix
i = 0, j = 0
push mat[i][j] value corresponding to key = {i - j}
= {0 - 0}
= 0
mat[i][j] = mat[0][0]
= 3
After this map would be:
key value
+-----+ +-----+
map = | 0 | -> | 3 |
+-----+ +-----+
i = 0, j = 1
push mat[i][j] value corresponding to key = {i - j}
= {0 - 1}
= -1
mat[i][j] = mat[0][1]
= 3
After this map would be:
key value
+-----+ +-----+
map = | 0 | -> | 3 |
+-----+ +-----+
| -1 | -> | 3 |
+-----+ +-----+
i = 0, j = 2
push mat[i][j] value corresponding to key = {i - j}
= {0 - 2}
= -2
mat[i][j] = mat[0][2]
= 1
After this map would be:
key value
+-----+ +-----+
map = | 0 | -> | 3 |
+-----+ +-----+
| -1 | -> | 3 |
+-----+ +-----+
| -2 | -> | 1 |
+-----+ +-----+
i = 0, j = 3
push mat[i][j] value corresponding to key = {i - j}
= {0 - 3}
= -3
mat[i][j] = mat[0][3]
= 1
After this map would be:
key value
+-----+ +-----+
map = | 0 | -> | 3 |
+-----+ +-----+
| -1 | -> | 3 |
+-----+ +-----+
| -2 | -> | 1 |
+-----+ +-----+
| -3 | -> | 1 |
+-----+ +-----+
i = 1, j = 0
push mat[i][j] value corresponding to key = {i - j}
= {1 - 0}
= 1
mat[i][j] = mat[1][0]
= 2
After this map would be:
key value
+-----+ +-----+
map = | 0 | -> | 3 |
+-----+ +-----+
| -1 | -> | 3 |
+-----+ +-----+
| -2 | -> | 1 |
+-----+ +-----+
| -3 | -> | 1 |
+-----+ +-----+
| 1 | -> | 2 |
+-----+ +-----+
i = 1, j = 1
push mat[i][j] value corresponding to key = {i - j}
= {1 - 1}
= 0
mat[i][j] = mat[1][1]
= 2
After this map would be:
key value
+-----+ +-----+-----+
map = | 0 | -> | 3 | 2 |
+-----+ +-----+-----+
| -1 | -> | 3 |
+-----+ +-----+
| -2 | -> | 1 |
+-----+ +-----+
| -3 | -> | 1 |
+-----+ +-----+
| 1 | -> | 2 |
+-----+ +-----+
Keep Doing this until i < rows and j < columns,
means to traverse the whole matrix.
After this whole step below would be the map's values:
key value
+-----+ +-----+-----+-----+
map = | 0 | -> | 3 | 2 | 1 |
+-----+ +-----+-----+-----+
| -1 | -> | 3 | 1 | 2 |
+-----+ +-----+-----+-----+
| -2 | -> | 1 | 2 |
+-----+ +-----+-----+
| -3 | -> | 1 |
+-----+ +-----+-----+
| 1 | -> | 2 | 1 |
+-----+ +-----+-----+
| 2 | -> | 1 |
+-----+ +-----+Sort each diagonal vector in the map:
Before Sorting:
key value
+-----+ +-----+-----+-----+
map = | 0 | -> | 3 | 2 | 1 |
+-----+ +-----+-----+-----+
| -1 | -> | 3 | 1 | 2 |
+-----+ +-----+-----+-----+
| -2 | -> | 1 | 2 |
+-----+ +-----+-----+
| -3 | -> | 1 |
+-----+ +-----+-----+
| 1 | -> | 2 | 1 |
+-----+ +-----+-----+
| 2 | -> | 1 |
+-----+ +-----+
After sorting:
key value
+-----+ +-----+-----+-----+
map = | 0 | -> | 1 | 2 | 3 |
+-----+ +-----+-----+-----+
| -1 | -> | 1 | 2 | 3 |
+-----+ +-----+-----+-----+
| -2 | -> | 1 | 2 |
+-----+ +-----+-----+
| -3 | -> | 1 |
+-----+ +-----+-----+
| 1 | -> | 1 | 2 |
+-----+ +-----+-----+
| 2 | -> | 1 |
+-----+ +-----+Rebuild the matrix by putting sorted elements back in the diagonals:
Sorted Map:
key value
+-----+ +-----+-----+-----+
map = | 0 | -> | 1 | 2 | 3 |
+-----+ +-----+-----+-----+
| -1 | -> | 1 | 2 | 3 |
+-----+ +-----+-----+-----+
| -2 | -> | 1 | 2 |
+-----+ +-----+-----+
| -3 | -> | 1 |
+-----+ +-----+-----+
| 1 | -> | 1 | 2 |
+-----+ +-----+-----+
| 2 | -> | 1 |
+-----+ +-----+
+------+------+------+------+
mat = | 1 | 1 | 1 | 1 |
+------+------+------+------+
[0, 0] [0, 1] [0, 2] [0, 3]
+------+------+------+------+
| 1 | 2 | 2 | 2 |
+------+------+------+------+
[1, 0] [1, 1] [1, 2] [1, 3]
+------+------+------+------+
| 1 | 2 | 3 | 3 |
+------+------+------+------+
[2, 0] [2, 1] [2, 2] [2, 3]Code:
#include <iostream>
#include <vector>
#include <unordered_map>
#include <algorithm>
using namespace std;
vector<vector<int>> diagonalSort(vector<vector<int>>& mat) {
unordered_map<int, vector<int>> diagonals;
int n = mat.size(); // Number of rows
int m = mat[0].size(); // Number of columns
// Step 1: Push elements into the corresponding diagonal in the map.
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
diagonals[i - j].push_back(mat[i][j]); // i - j gives the diagonal key
}
}
// Step 2: Sort each diagonal in the map.
for (auto& diag : diagonals) {
sort(diag.second.begin(), diag.second.end());
}
// Step 3: Rebuild the matrix by putting sorted elements back in the diagonals.
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
mat[i][j] = diagonals[i - j].front(); // Take the front element
diagonals[i - j].erase(diagonals[i - j].begin()); // Pop the front element
}
}
return mat;
}
// Helper function to print the matrix
void printMatrix(const vector<vector<int>>& mat) {
for (const auto& row : mat) {
for (int elem : row) {
cout << elem << " ";
}
cout << endl;
}
}
int main() {
vector<vector<int>> mat = {
{3, 3, 1, 1},
{2, 2, 1, 2},
{1, 1, 1, 2}
};
cout << "Original matrix:\n";
printMatrix(mat);
vector<vector<int>> sortedMat = diagonalSort(mat);
cout << "\nMatrix after diagonal sorting:\n";
printMatrix(sortedMat);
return 0;
}
Explanation:
- We use an unordered map
diagonalsto group elements of each diagonal based on the keyi - j. - We sort the values in each diagonal using
sort(). - We then reassign the sorted values back to the appropriate diagonal positions in the matrix by popping the elements from the back of the list (to ensure correct order).
Complexity Analysis:
Time Complexity Analysis:
- Grouping Diagonal Elements:
- We iterate over each element of the matrix exactly once to group the elements into diagonals.
- The number of elements in the matrix is
m * n. - So, the time complexity for this step is O(m * n).
- Sorting Diagonal Elements:
- For each diagonal, we sort the list of elements. There are at most
min(m, n)elements in any diagonal. - Sorting each diagonal takes
O(d * log d)time, wheredis the length of the diagonal. - The total number of elements across all diagonals is
m * n, so the total sorting time across all diagonals is O(m * n * log(min(m, n))).
- For each diagonal, we sort the list of elements. There are at most
- Placing Sorted Elements Back:
- We again iterate through the matrix to place the sorted elements back, which takes O(m * n).
Overall Time Complexity:
- Grouping: O(m * n)
- Sorting: O(m * n * log(min(m, n)))
- Placing back: O(m * n)
Thus, the overall time complexity is O(m * n * log(min(m, n))).
Space Complexity:
- We are using a hash map to store the diagonals, which requires extra space proportional to the number of elements in the matrix, i.e., O(m * n).
2️⃣ Priority Queue (Min-Heap) Approach:
An alternative approach is to use a priority queue (min-heap) for each diagonal. Instead of sorting the diagonal explicitly using sort(), we can push elements into a min-heap, which maintains the sorted order. Then, we pop from the heap to place the sorted elements back into the matrix.
- Group elements by diagonal using a priority queue (min-heap).
- For each diagonal, insert elements into the heap.
- Pop from the heap and place elements back into the matrix.
Advantages:
- Sorting using a heap is efficient for online processing (if we need partial sorting).
Code:
#include <iostream>
#include <vector>
#include <unordered_map>
#include <queue>
using namespace std;
vector<vector<int>> diagonalSortHeap(vector<vector<int>>& mat) {
int m = mat.size();
int n = mat[0].size();
// Map to store min-heaps for each diagonal.
unordered_map<int, priority_queue<int, vector<int>, greater<int>>> diagonals;
// Step 1: Push elements into the heap (group by diagonals).
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
diagonals[i - j].push(mat[i][j]);
}
}
// Step 2: Put sorted values back into the matrix by popping from the heap.
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
mat[i][j] = diagonals[i - j].top();
diagonals[i - j].pop();
}
}
return mat;
}
// Helper function to print the matrix
void printMatrix(const vector<vector<int>>& mat) {
for (const auto& row : mat) {
for (int elem : row) {
cout << elem << " ";
}
cout << endl;
}
}
int main() {
vector<vector<int>> mat = {
{3, 3, 1, 1},
{2, 2, 1, 2},
{1, 1, 1, 2}
};
cout << "Original matrix:\n";
printMatrix(mat);
vector<vector<int>> sortedMat = diagonalSortHeap(mat);
cout << "\nMatrix after diagonal sorting:\n";
printMatrix(sortedMat);
return 0;
}Complexity Analysis:
Time Complexity:
- Grouping elements into diagonals using a min-heap:
- We traverse the matrix and for each diagonal, we insert elements into a min-heap (which maintains the sorted order).
- Time Complexity: Inserting
kelements into a heap takes O(k * log k), wherekis the number of elements. Since we are inserting all elements of a diagonal into a heap, the total cost for all elements in the matrix is O(m * n * log(min(m, n))).
- Rebuilding the matrix:
- After the diagonals are sorted using heaps, we pop elements from the min-heap and put them back into the matrix. This requires visiting each element again.
- Time Complexity: This step takes O(m * n).
Total Time Complexity:
- Inserting into heaps: O(m * n * log(min(m, n)))
- Rebuilding the matrix: O(m * n)
Thus, the overall time complexity: O(m * n * log(min(m, n)))
Space Complexity:
- We are using a
priority_queue(min-heap) for each diagonal. In the worst case, each diagonal can havemin(m, n)elements, and there arem * nelements in total. Hence, the space complexity is O(m * n) for the heaps
