Problem Statement

Given the root of a binary tree, the task is to return the vertical order traversal of its nodes' values. Nodes should be reported from top to bottom and left to right within the same level and vertical line.

The vertical order of a binary tree is defined as follows:

1. Each column corresponds to a vertical line in the tree, starting from the root node.
2. Columns are indexed, with the root node located at column 0.
   • Moving left decrements the column index by 1.
   • Moving right increments the column index by 1.
   • The left and right children of a node at location (row, col) will be at (row + 1, col - 1) and (row + 1, col + 1), respectively. The tree's root is located at (0, 0).
3. If two nodes are in the same column and level, the node with the smaller value comes first in the traversal.

Examples

Example 1:

Input: 
        3
       / \
      9   20
          /  \
         15   7

Output: [
         [9],
         [3, 15],
         [20],
         [7]
        ]

Explanation:
The column -1 contains [9].
The column 0 contains [3, 15].
The column 1 contains [20].
The column 2 contains [7].

Example 2:

Input:
        1
       / \
      2   3
     /|   |\
    4 5   6 7

Output: [
         [4],
         [2],
         [1, 5, 6],
         [3],
         [7]
        ]

Explanation:
The column -2 contains [4].
The column -1 contains [2].
The column 0 contains [1, 5, 6].
The column 1 contains [3].
The column 2 contains [7].

Different Approaches

1️⃣ Horizontal Distance 

Intuition:

The vertical order traversal of a binary tree involves organizing nodes based on their horizontal and vertical positions relative to their parent nodes. Each node can be categorized by its vertical column ('x') and level ('y'). Nodes with the same 'x' value are aligned vertically, forming columns, while 'y' represents the depth or level within the tree.

To achieve this traversal, use a level order BFS approach, starting from the root node. This ensures that nodes are processed level by level, and within each level, nodes are processed from left to right. By maintaining a map structure that uses 'x' as keys for vertical columns and 'y' as keys within a nested map for levels, we store node values in a multiset to maintain uniqueness and sorting.

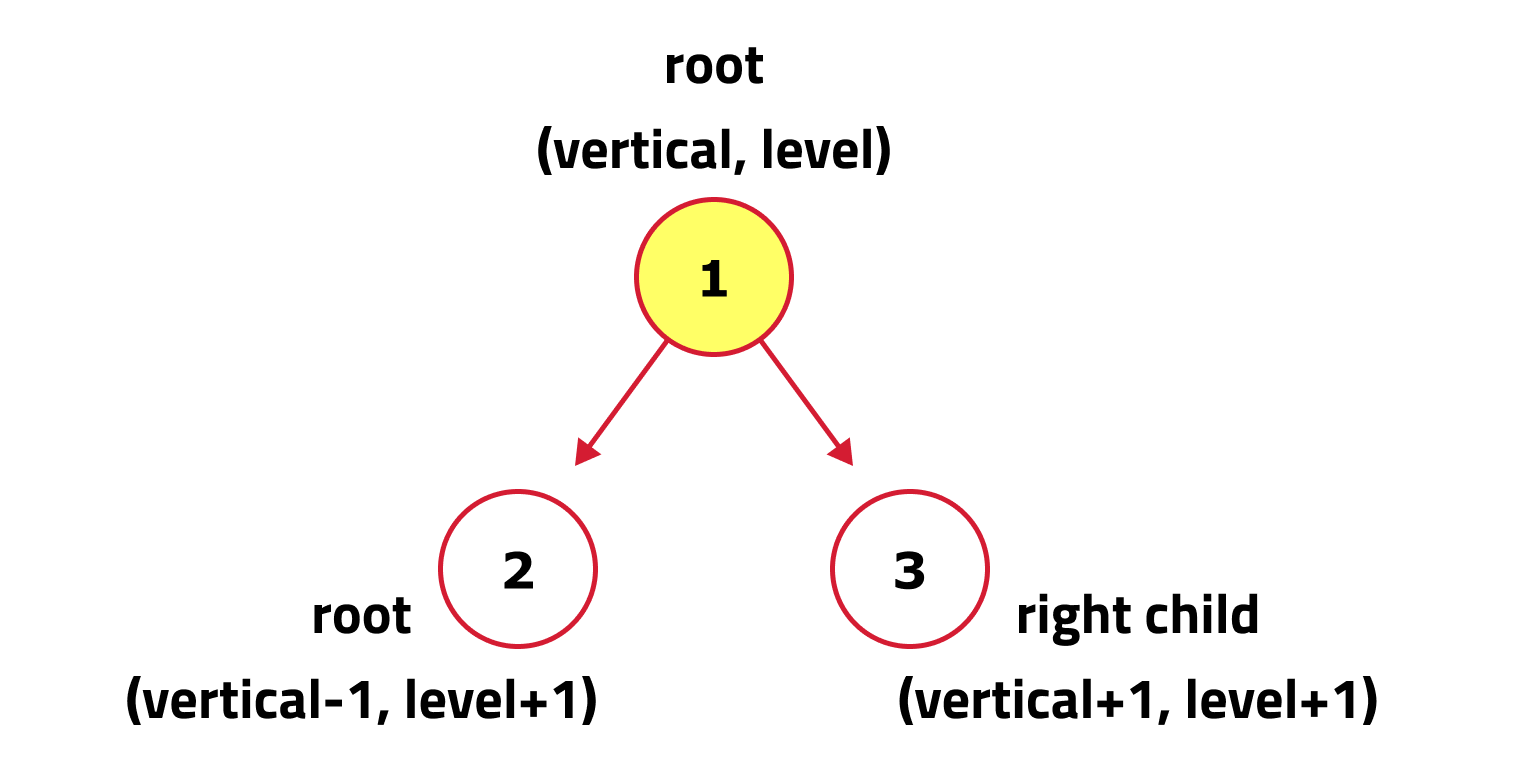
Approach:

1. Begin by initializing an empty map to store nodes according to their 'x' (vertical column) and 'y' (level) coordinates. Utilize a multiset within this map to maintain the correct order of nodes that fall under the same vertical column and level.
2. Set up a queue for performing a breadth-first search (BFS) traversal of the tree, starting with the root node positioned at coordinates (0, 0), where '0' represents the root's vertical column and level.
3. While the queue is not empty, perform the following steps: dequeue a node, and record its value in the map at its corresponding 'x' and 'y' coordinates. Then, enqueue the left and right children of the node with updated coordinates: the left child is enqueued with 'x' decremented by 1 and 'y' incremented by 1, while the right child is enqueued with 'x' incremented by 1 and 'y' incremented by 1.
4. After completing the BFS traversal, process the map to create a list of node values for each vertical column. This involves iterating through the map, collecting values from the multiset for each vertical column, and assembling these values into column vectors.
5. Finally, compile these column vectors into a 2D vector that represents the vertical order traversal of the binary tree, ensuring that nodes are ordered by their vertical column positions.

Code:

 #include<bits/stdc++.h>
using namespace std;

struct TreeNode {
    int data;
    TreeNode* left;
    TreeNode* right;
    TreeNode(int val) : data(val), left(nullptr), right(nullptr) {}
};

class Solution {
public:
    vector<vector<int>> verticalTraversal(TreeNode* root) {
        // List to store the final result
        vector<vector<int>> result;

        if (root == nullptr) {
            return result;
        }

        // Map to store the nodes at each vertical distance and level
        map<int, map<int, priority_queue<int, vector<int>, greater<int>>>> nodesMap;

        // Queue for BFS traversal (stores node along with its x and y coordinates)
        queue<pair<TreeNode*, pair<int, int>>> q;
        q.push({root, {0, 0}});  // (node, {x, y})

        // Perform BFS
        while (!q.empty()) {
            auto p = q.front();
            q.pop();
            TreeNode* node = p.first;
            int x = p.second.first;
            int y = p.second.second;

            // Add the node's value to the map at the correct x and y
            nodesMap[x][y].push(node->data);

            // Add the left child with updated coordinates to the queue
            if (node->left != nullptr) {
                q.push({node->left, {x - 1, y + 1}});
            }

            // Add the right child with updated coordinates to the queue
            if (node->right != nullptr) {
                q.push({node->right, {x + 1, y + 1}});
            }
        }

        // Prepare the result by sorting keys and compiling nodes
        for (auto& p : nodesMap) {
            vector<int> column;
            for (auto& q : p.second) {
                while (!q.second.empty()) {
                    column.push_back(q.second.top());
                    q.second.pop();
                }
            }
            result.push_back(column);
        }

        return result;
    }
};


// Main method to test the verticalTraversal function
int main() {
    // Creating a binary tree
    TreeNode* root = new TreeNode(1);
    root->left = new TreeNode(2);
    root->right = new TreeNode(3);
    root->left->left = new TreeNode(4);
    root->left->right = new TreeNode(5);
    root->right->left = new TreeNode(6);
    root->right->right = new TreeNode(7);

    // Creating an instance of Solution
    Solution sol;

    // Getting the vertical order traversal
    vector<vector<int>> result = sol.verticalTraversal(root);

    // Printing the result
    cout << "Vertical Order Traversal: " << endl;
    for (const auto& col : result) {
        for (int num : col) {
            cout << num << " ";
        }
        cout << endl;
    }

    return 0;
}

Complexity Analysis:

• Time Complexity: O(N * log2N * log2N * log2N): This complexity arises from performing postorder traversal using BFS, where each node's insertion and retrieval operations in nested maps take logarithmic time. Overall, it reflects the combined cost of processing each node and managing the node mappings.
• Space Complexity: O(N + N/2): The space usage is dominated by the map storing nodes by their vertical and level information, occupying O(N) space. Additionally, the queue for BFS can occupy up to O(N/2) space in a balanced tree's worst-case scenario, contributing to the total space complexity.