Problem Statement
Given an array arr of n integers, return true if the array can be partitioned into two subsets such that the sum of elements in both subsets is equal else return false.
LeetCode:
Constraints:
1 <= nums.length <= 200
1 <= nums[i] <= 1001 ≤ nums.length ≤ 200- The array
numsmust contain at least 1 and at most 200 elements. - This tells us the input size we are working with. A maximum of 200 is relatively small, so algorithms with time complexity up to
O(n^2)(nested loops) are generally acceptable.
- The array
1 ≤ nums[i] ≤ 100- Each element of the nums array is a positive integer between 1 and 100, inclusive.
- No need to handle negative or zero values.
- The range is small, which may allow optimization techniques like counting arrays, prefix sums, or frequency maps.
Examples
Example 1:
Input: arr = [1, 10, 21, 10]
Output: True
Explanation: The array can be partitioned as [1, 10, 10] and [21]Example 2:
Input: arr = [1, 2, 3, 5]
Output: False
Explanation: The array cannot be partitioned into equal sum subsets.Different Approaches
1️⃣ Recursive Approach
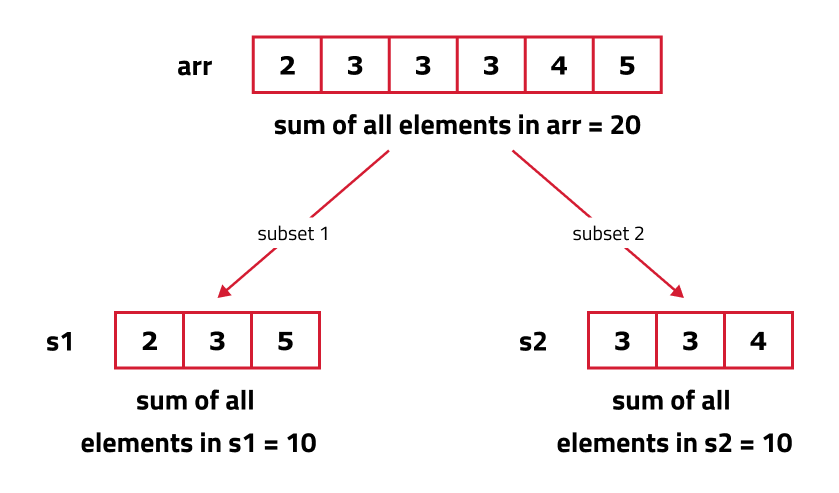
This question is a slight modification of the problem discussed in Subset-sum equal to target. We need to partition the array(say S) into two subsets(say S1 and S2). According to the question:
- Sum of elements of S1 + sum of elements of S2 = sum of elements of S.
- Sum of elements of S1 = sum of elements of S2.
- These two conditions imply that S1 = S2 = (S/2).
Observation:
- If S (sum of elements of the input array) is odd , there is no way we can divide it into two equal halves, so we can simply return false.
- If S is even, then we need to find a subset in the input array whose sum is equal to S/2 because if we find one subset with sum S/2, the remaining elements sum will be automatically S/2. So, we can partition the given array. Hence we return true.
From here try to find a subset in the array with target = S/2 as discussed in Subset-sum equal to target.
The idea is to generate all pssible subsets and whenever a single subsets is found whose sum is equal to the given target(S/2), simply return true. As, all the subsets needs to generated, recursion can be used to solve this problem.
Steps to form the recursive solution:
- Express the problem in terms of indexes: The array will have an index but there is one more parameter “target”. So, we can say that initially, we need to find(n-1, target) which means that we need to find whether there exists a subset in the array from index 0 to n-1, whose sum is equal to the target.
- So, f(ind, target) will check whether a subset exists in the array from index 0 to index 'ind' such that the sum of elements is equal to the target.
- Try out all possible choices at a given index: As all the subsets needs to be generated, we will use the pick/non-pick technique. There will be two choices in each function call:
- Do not include the current element in the subset: First try to find a subset without considering the current index element. For this, make a recursive call to f(ind-1,target).
- Include the current element in the subset: Now try to find a subset by considering the current index element as part of subset. As the current element(arr[ind]) is included, the remaining target sum will be target - arr[ind]. Therefore, make a function call of f(ind-1,target-arr[ind]).
Note: Consider the current element in the subset only when the current element is less or equal to the target.
/*It is pseudocode and it is not tied to
any specific programming language*/
f(ind, target){
not pick = f(ind-1, target)
pick = false
if(target <= arr[ind]{
pick = f(ind-1, target - arr[ind])
}
}- Return (pick || not pick): As we are looking for only one subset whose sum of elements is equal to target, if any of the one among 'pick' or 'not pick' returns true, it means the required subset is found so, return true.
/*It is pseudocode and it is not tied to
any specific programming language*/
f(ind, target){
not pick = f(ind-1, target)
pick = false
if(target <= arr[ind]{
pick = f(ind-1, target - arr[ind])
}
return (pick || not pick)
}- Base cases: There will be two base cases.
- First, when target == 0, it means that the subset is already found from the previous steps, so simply return true.
- Another, when ind==0, it means we are at the first element, so return arr[ind]==target. If the element is equal to the target it will return true else false.
Code:
Starting from the end of the array:
#include <bits/stdc++.h>
using namespace std;
class Solution {
private:
/* Function to determine if it's possible to form a subset
with the given target sum using elements up to the current index */
bool canFormSubset(int currentIndex, int targetSum, vector<int>& nums) {
// Base case: If the target sum is 0, a valid subset is found
if (targetSum == 0)
return true;
// Base case: If we are at the first element, check if it equals the target sum
if (currentIndex == 0)
return nums[0] == targetSum;
// Option 1: Exclude the current element
bool excludeCurrent = canFormSubset(currentIndex - 1, targetSum, nums);
// Option 2: Include the current element (only if it does not exceed the target sum)
bool includeCurrent = false;
if (nums[currentIndex] <= targetSum)
includeCurrent = canFormSubset(currentIndex - 1, targetSum - nums[currentIndex], nums);
// Return true if either option is successful
return excludeCurrent || includeCurrent;
}
public:
/* Function to check if the array can be partitioned into
two subsets with equal sum */
bool canPartition(vector<int>& nums) {
int totalSum = 0;
// Calculate the total sum of the array
for (int num : nums) {
totalSum += num;
}
// If the total sum is odd, it cannot be partitioned into two equal subsets
if (totalSum % 2 != 0)
return false;
// Target sum for each subset (half of the total sum)
int targetSum = totalSum / 2;
// Call the helper function to check if a subset with the target sum exists
return canFormSubset(nums.size() - 1, targetSum, nums);
}
};
int main() {
vector<int> nums = {2, 3, 3, 3, 4, 5};
int n = nums.size();
// Create an instance of the Solution class
Solution sol;
// Check if the array can be partitioned into two equal subsets
if (sol.canPartition(nums))
cout << "The array can be partitioned into two equal subsets" << endl;
else
cout << "The array cannot be partitioned into two equal subsets" << endl;
return 0;
}Starting from the beginning of the array:
class Solution {
public:
bool recursive(vector<int>& nums, int index, int target) {
// Base Cases
if (target == 0) return true;
if (index >= nums.size() || target < 0) return false;
// Pick the number
bool include = recursive(nums, index + 1, target - nums[index]);
// Skip the number
bool exclude = recursive(nums, index + 1, target);
return include || exclude;
}
bool canPartition(vector<int>& nums) {
int sum = accumulate(nums.begin(), nums.end(), 0);
// If total sum is odd, cannot split equally
if (sum % 2 != 0) return false;
int target = sum / 2;
return recursive(nums, 0, target);
}
};
Complexity Analysis:
- Time Complexity:
O(2^(N)), whereNis the length of the array. As, for each index, there are two possible options. - Space Complexity:
O(N), at maximum the depth of the recursive stack can go up to N.
2️⃣ Memoization
In order to convert a recursive solution to memoization the following steps will be taken:
Declare a dp array of size [n][target+1]: As there are two changing parameters in the recursive solution, 'ind' and 'target'. The maximum value 'ind' can attain is (n), where n is the size of array and for 'target' only values between 0 to target. Therefore, we need 2D dp array.
The dp array stores the calculations of subproblems. Initialize dp array with -1, to indicate that no subproblem has been solved yet.
- While encountering an overlapping subproblem: When we come across a subproblem, for which the dp array has value other than -1, it means we have found a subproblem which has been solved before hence it is an overlapping subproblem. No need to calculate it's value again just retrieve the value from dp array and return it.
- Store the value of subproblem: Whenever, a subproblem is encountered and it is not solved yet(the value at this index will be -1 in the dp array), store the calculated value of subproblem in the array.
Code:
#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
bool recursive(int index, int target, vector<int>& nums, vector<vector<int>>& dp) {
// Base Cases
if (target == 0) return true; // Found a valid subset
if (index >= nums.size()) return false;
// If already computed
if (dp[index][target] != -1) return dp[index][target];
// Include current number if it's not bigger than target
bool include = false;
if (nums[index] <= target) {
include = recursive(index + 1, target - nums[index], nums, dp);
}
// Exclude current number
bool exclude = recursive(index + 1, target, nums, dp);
return dp[index][target] = include || exclude;
}
bool canPartition(vector<int>& nums) {
int sum = accumulate(nums.begin(), nums.end(), 0);
// If total sum is odd, we can't partition it equally
if (sum % 2 != 0) return false;
int target = sum / 2;
int n = nums.size();
// Create memoization table
vector<vector<int>> dp(n, vector<int>(target + 1, -1));
return recursive(0, target, nums, dp);
}
};
Complexity Analysis:
- Time Complexity:
O(n * target) - Space Complexity:
O(n * target) + O(n)
3️⃣ Tabulation
In order to convert a recursive code to tabulation code, we try to convert the recursive code to tabulation and here are the steps:
- Declare a dp array of size [n][target+1]: As there are two changing parameters in the recursive solution, 'ind' and 'target'. The maximum value 'ind' can attain is (n) and including 0 its n, where n is the size of array, for 'target' can have any values between 0 to 'target'. So we need a 2D dp array. Set its type as bool and initialize it as false.
- Setting Base Cases in the Array: In the recursive code, our base condition was when target == 0, it means the required subset is found and we were returning true. So, set 'true' in the dp array for every index where target = 0.
- The first row dp[0][] indicates that only the first element of the array is considered, therefore for the target value equal to arr[0], only cell with that target will be true, so explicitly set dp[0][arr[0]] =true, (dp[0][arr[0]] means that we are considering the first element of the array with the target equal to the first element itself). Please note that it can happen that arr[0]>target, so we first check it: if(arr[0]<=target) then set dp[0][arr[0]] = true.
- Iterative Computation Using Loops: Initialize two nested for loops to traverse the dp array and following the logic discussed in the recursive approach, set the value of each cell in the 2D dp array. Instead of recursive calls, use the dp array itself to find the values of intermediate calculations.
- Returning the answer: At last dp[n-1][target] will hold the solution after the completion of whole process, as we are doing the calculations in bottom-up manner.
Code:
#include <bits/stdc++.h>
using namespace std;
class Solution{
private:
/* Function to check if it's possible to partition
the array into two subsets with equal sum*/
bool func(int ind, int target, int n, vector<int> &arr) {
int totSum = 0;
// Calculate the total sum of the array
for (int i = 0; i < n; i++) {
totSum += arr[i];
}
/* If the total sum is odd, it cannot
be partitioned into two equal subsets*/
if (totSum % 2 == 1)
return false;
else {
int k = totSum / 2;
/* Create a DP table with dimensions
n x k+1, initialized with false*/
vector<vector<bool>> dp(n, vector<bool>(k + 1, false));
/* Base case: If the target sum is 0, it
can be achieved by not selecting any elements*/
for (int i = 0; i < n; i++) {
dp[i][0] = true;
}
/* Initialize the first row based
on the first element of the array*/
if (arr[0] <= k)
dp[0][arr[0]] = true;
// Fill in the DP table using bottom-up approach
for (int ind = 1; ind < n; ind++) {
for (int target = 1; target <= k; target++) {
// Exclude the current element
bool notTaken = dp[ind - 1][target];
/* Include the current element if
it doesn't exceed the target*/
bool taken = false;
if (arr[ind] <= target)
taken = dp[ind - 1][target - arr[ind]];
// Update the DP table
dp[ind][target] = notTaken || taken;
}
}
/* The final result is in
the last cell of the DP table*/
return dp[n - 1][k];
}
}
public:
/* Function to check if the array can
be partitioned into two equal subsets*/
bool equalPartition(int n, vector<int>& arr) {
int totSum = 0;
// Calculate the total sum of the array
for (int i = 0; i < n; i++) {
totSum += arr[i];
}
/* If the total sum is odd, it cannot
be partitioned into two equal subsets*/
if (totSum % 2 == 1)
return false;
else{
int k = totSum / 2;
// Return the result
return func(n - 1, k, n, arr);
}
}
};
int main() {
vector<int> arr = {2, 3, 3, 3, 4, 5};
int n = arr.size();
//Create an instance of Solution class
Solution sol;
if (sol.equalPartition(n, arr))
cout << "The Array can be partitioned into two equal subsets";
else
cout << "The Array cannot be partitioned into two equal subsets";
return 0;
}
Complexity Analysis:
- Time Complexity:
O(n*target) - Space Complexity:
O(n*target)
4️⃣ Space Optimized Approach
Steps to space optimize the tabulation approach:
- Decalre an array to store the previous row of the DP table. Initialize the first row and first column of the DP table based on the base conditions discussed in tabulation.
- Now, initiate two nested loops in bottom-up approach. The first loop will run for 'ind' and the second loop will run for the 'target' variable.
- In order to store the current row of the DP table, initialize a new array 'cur' and fill the first cell to 'true' for base condition.
- Do the calculations for 'cur' row by performing the pick/non-pick technique used in previous approaches.
- Now, update the previous row with the current row for the next iteration and at last return the final result stored in the last cell of the previous row(prev[k]).
Code:
#include <bits/stdc++.h>
using namespace std;
class Solution{
private:
/* Function to check if it's possible to partition
the array into two subsets with equal sum*/
bool func(int n, vector<int> &arr) {
int totSum = 0;
// Calculate the total sum of the array
for (int i = 0; i < n; i++) {
totSum += arr[i];
}
/* If the total sum is odd, it cannot
be partitioned into two equal subsets*/
if (totSum % 2 == 1)
return false;
else {
int k = totSum / 2;
/* Create a vector to represent
the previous row of the DP table*/
vector<bool> prev(k + 1, false);
/* Base case: If the target sum is 0, it can
be achieved by not selecting any elements*/
prev[0] = true;
/* Initialize the first row based
on the first element of the array*/
if (arr[0] <= k)
prev[arr[0]] = true;
/* Fill in the DP table
using a bottom-up approach*/
for (int ind = 1; ind < n; ind++) {
/* Initialize a vector to represent
the current row of the DP table*/
vector<bool> cur(k + 1, false);
cur[0] = true;
for (int target = 1; target <= k; target++) {
// Exclude the current element
bool notTaken = prev[target];
/* Include the current element
if it doesn't exceed the target*/
bool taken = false;
if (arr[ind] <= target)
taken = prev[target - arr[ind]];
// Update the current row of the DP table
cur[target] = notTaken || taken;
}
/* Set the current row as the
previous row for the next iteration*/
prev = cur;
}
/* The final result is in the last cell
of the previous row of the DP table*/
return prev[k];
}
}
public:
/* Function to check if the array can
be partitioned into two equal subsets*/
bool equalPartition(int n, vector<int>& arr) {
// Return the result
return func(n, arr);
}
};
int main() {
vector<int> arr = {2, 3, 3, 3, 4, 5};
int n = arr.size();
//Create an instance of Solution class
Solution sol;
if (sol.equalPartition(n, arr))
cout << "The Array can be partitioned into two equal subsets";
else
cout << "The Array cannot be partitioned into two equal subsets";
return 0;
}
Complexity Analysis:
- Time Complexity:
O(N*target), where target is the total sum of elements of the array divided by 2. As, here are three nested loops that account for O(N*target) complexity. - Space Complexity:
O(target), As arrays of size (target+1) is used.
