Problem Statement
You are given a 2D grid of size m x n representing a box, and you have n balls. The box is open on both the top and bottom sides. Each cell in the box has a diagonal board that can either redirect a ball to the right or to the left.
- A board that redirects the ball to the right spans from the top-left to the bottom-right corner of the cell, and it is represented in the grid as
1. - A board that redirects the ball to the left spans from the top-right to the bottom-left corner of the cell, and it is represented in the grid as
-1.
You will drop one ball from the top of each column in the box. The ball may:
- Continue moving through the grid based on the diagonal boards.
- Get stuck if it encounters a "V" shaped pattern or hits the wall of the grid.
- Fall out of the bottom of the grid.
Your task is to return an array answer of size n where answer[i] is the column number where the ball dropped from column i falls out, or -1 if the ball gets stuck.
Examples
Example 1: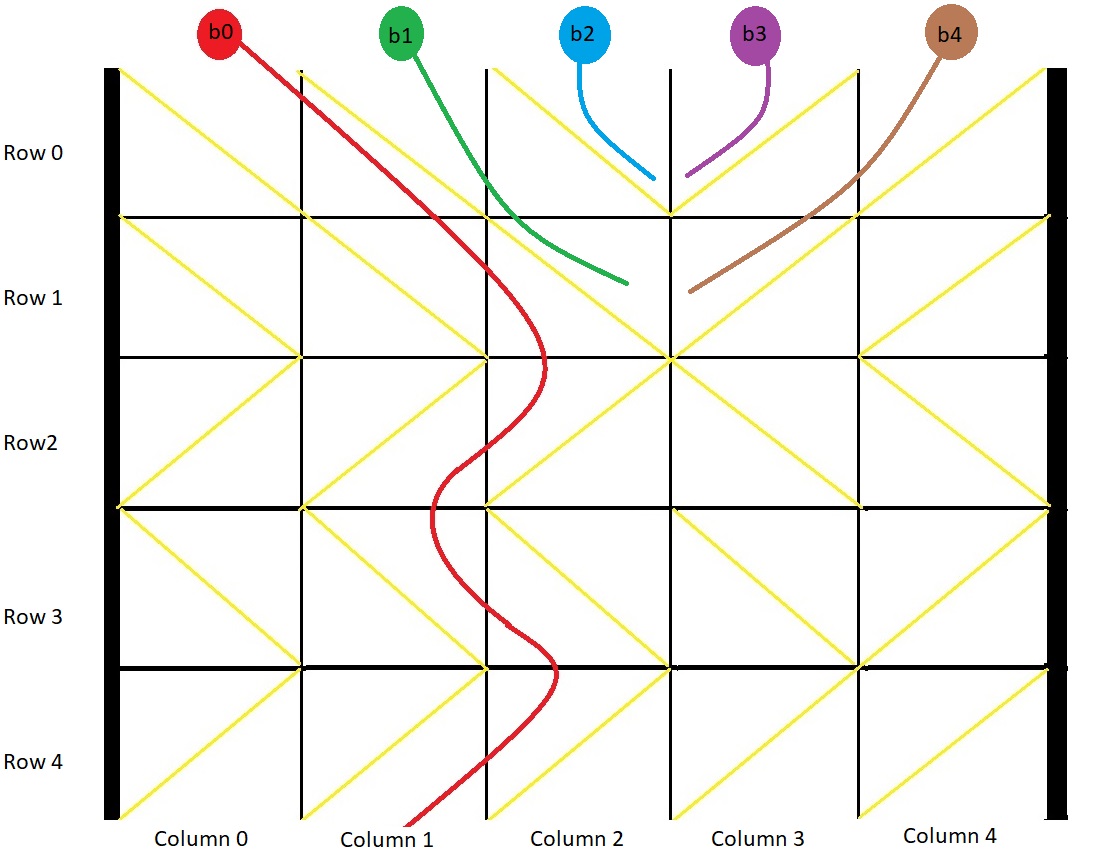
Input: grid = [[1,1,1,-1,-1],[1,1,1,-1,-1],[-1,-1,-1,1,1],[1,1,1,1,-1],[-1,-1,-1,-1,-1]]
Output: [1,-1,-1,-1,-1]
Explanation: This example is shown in the photo.
Ball b0 is dropped at column 0 and falls out of the box at column 1.
Ball b1 is dropped at column 1 and will get stuck in the box between column 2 and 3 and row 1.
Ball b2 is dropped at column 2 and will get stuck on the box between column 2 and 3 and row 0.
Ball b3 is dropped at column 3 and will get stuck on the box between column 2 and 3 and row 0.
Ball b4 is dropped at column 4 and will get stuck on the box between column 2 and 3 and row 1Example 2:
Input: grid = [
[-1]
]
Output: [-1]
Explanation: The ball get stuck agains the left wall.Example 3:
Input: grid = [
[ 1, 1, 1, 1, 1, 1],
[-1,-1,-1,-1,-1,-1],
[ 1, 1, 1, 1, 1, 1],
[-1,-1,-1,-1,-1,-1]
]
Output: [0, 1, 2, 3, 4, -1]
Explanation: The ball dropped from column 5 gets stuck, while the others fall out of the grid.Different Approaches
1️⃣ Simulate Ball Movement
Intuition:
To solve the problem, we simulate the movement of each ball through the grid:
- Start the ball at each column of the grid.
- At each row, decide the next column based on the direction indicated by the grid cell.
- A ball gets stuck if:
- It moves out of bounds.
- It encounters a "V" shape, where it cannot move either left or right.
- If the ball successfully reaches the bottom, record the column where it falls out.
Steps:
- Loop over each column, and simulate the movement of the ball row by row.
- For each ball, check if it can continue moving based on the direction of the current board and if the next column is valid.
- If the ball can move all the way to the last row, record the final column. If it gets stuck, return
-1for that ball.


Code:
class Solution {
public:
vector<int> findBall(vector<vector<int>>& grid) {
int m = grid.size();
int n = grid[0].size();
vector<int> result(n, -1); // Initialize result array with -1
for (int col = 0; col < n; col++) {
int current_col = col;
// Simulate ball movement row by row
for (int row = 0; row < m; row++) {
// Check direction of the board at (row, current_col)
if (grid[row][current_col] == 1) {
// If the ball moves right but hits a left-redirecting board or the right wall
if (current_col == n - 1 || grid[row][current_col + 1] == -1) {
current_col = -1;
break;
}
current_col++; // Move the ball to the right
} else {
// If the ball moves left but hits a right-redirecting board or the left wall
if (current_col == 0 || grid[row][current_col - 1] == 1) {
current_col = -1;
break;
}
current_col--; // Move the ball to the left
}
}
// If the ball is not stuck, update the result
if (current_col != -1) {
result[col] = current_col;
}
}
return result;
}
};
Complexity Analysis:
- Time Complexity:
- The outer loop iterates over all columns (
O(n)), and for each column, we traverse each row (O(m)). - The overall time complexity is O(m * n).
- The outer loop iterates over all columns (
- Space Complexity:
- We use extra space for the result array, which has size
n. Therefore, the space complexity is O(n).
- We use extra space for the result array, which has size
