Problem Statement

You are given a 2D grid of size m x n representing a box, and you have n balls. The box is open on both the top and bottom sides. Each cell in the box has a diagonal board that can either redirect a ball to the right or to the left.

• A board that redirects the ball to the right spans from the top-left to the bottom-right corner of the cell, and it is represented in the grid as 1.
• A board that redirects the ball to the left spans from the top-right to the bottom-left corner of the cell, and it is represented in the grid as -1.

You will drop one ball from the top of each column in the box. The ball may:

• Continue moving through the grid based on the diagonal boards.
• Get stuck if it encounters a "V" shaped pattern or hits the wall of the grid.
• Fall out of the bottom of the grid.

Your task is to return an array answer of size n where answer[i] is the column number where the ball dropped from column i falls out, or -1 if the ball gets stuck.

Examples

Example 1: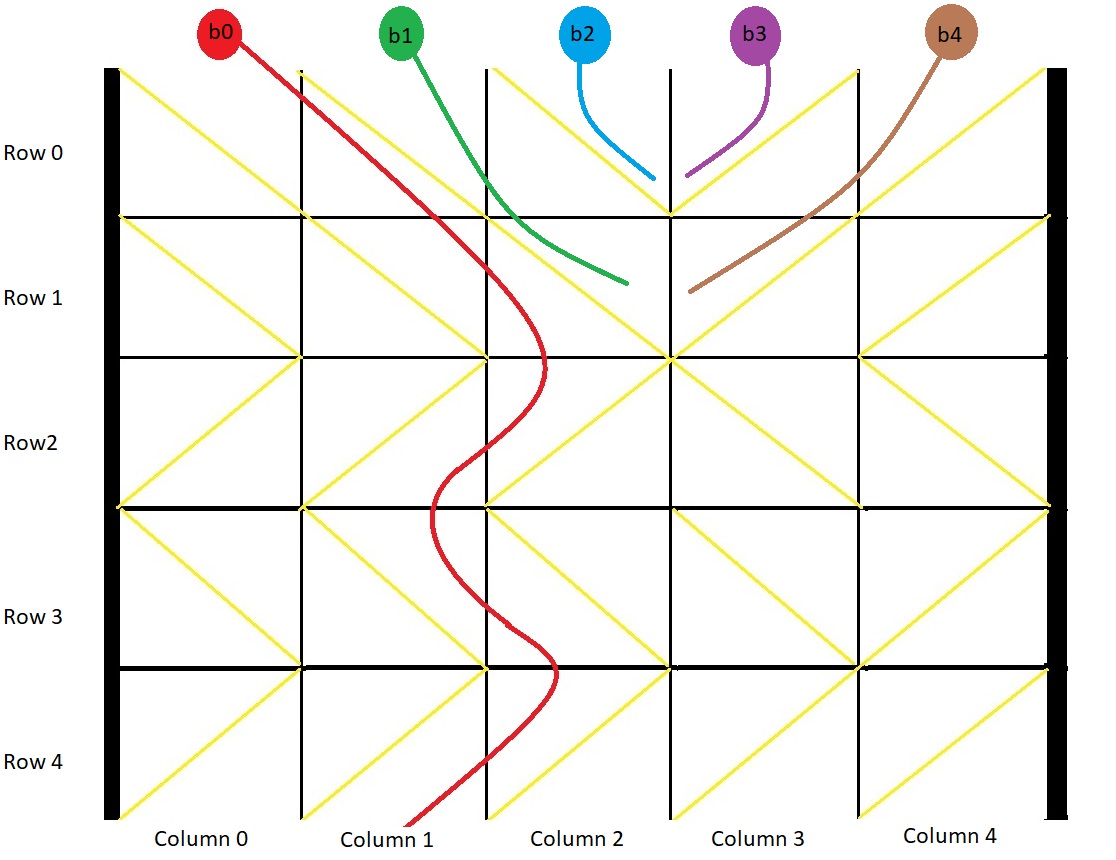

Input: grid = [[1,1,1,-1,-1],[1,1,1,-1,-1],[-1,-1,-1,1,1],[1,1,1,1,-1],[-1,-1,-1,-1,-1]]
Output: [1,-1,-1,-1,-1]
Explanation: This example is shown in the photo.
Ball b0 is dropped at column 0 and falls out of the box at column 1.
Ball b1 is dropped at column 1 and will get stuck in the box between column 2 and 3 and row 1.
Ball b2 is dropped at column 2 and will get stuck on the box between column 2 and 3 and row 0.
Ball b3 is dropped at column 3 and will get stuck on the box between column 2 and 3 and row 0.
Ball b4 is dropped at column 4 and will get stuck on the box between column 2 and 3 and row 1

Example 2:

Input: grid = [
               [-1]
              ]
Output: [-1]

Explanation: The ball get stuck agains the left wall.

Example 3:

Input: grid = [
               [ 1, 1, 1, 1, 1, 1],
               [-1,-1,-1,-1,-1,-1],
               [ 1, 1, 1, 1, 1, 1],
               [-1,-1,-1,-1,-1,-1]
              ]
Output: [0, 1, 2, 3, 4, -1]

Explanation: The ball dropped from column 5 gets stuck, while the others fall out of the grid.

Different Approaches

1️⃣ Simulate Ball Movement

Intuition:

To solve the problem, we simulate the movement of each ball through the grid:

1. Start the ball at each column of the grid.
2. At each row, decide the next column based on the direction indicated by the grid cell.
3. A ball gets stuck if:
   • It moves out of bounds.
   • It encounters a "V" shape, where it cannot move either left or right.
4. If the ball successfully reaches the bottom, record the column where it falls out.

Steps:

1. Loop over each column, and simulate the movement of the ball row by row.
2. For each ball, check if it can continue moving based on the direction of the current board and if the next column is valid.
3. If the ball can move all the way to the last row, record the final column. If it gets stuck, return -1 for that ball.

Code:

class Solution {
public:
    vector<int> findBall(vector<vector<int>>& grid) {
        int m = grid.size();
        int n = grid[0].size();
        
        vector<int> result(n, -1); // Initialize result array with -1
        
        for (int col = 0; col < n; col++) {
            int current_col = col;
            
            // Simulate ball movement row by row
            for (int row = 0; row < m; row++) {
                // Check direction of the board at (row, current_col)
                if (grid[row][current_col] == 1) {
                    // If the ball moves right but hits a left-redirecting board or the right wall
                    if (current_col == n - 1 || grid[row][current_col + 1] == -1) {
                        current_col = -1;
                        break;
                    }
                    current_col++; // Move the ball to the right
                } else {
                    // If the ball moves left but hits a right-redirecting board or the left wall
                    if (current_col == 0 || grid[row][current_col - 1] == 1) {
                        current_col = -1;
                        break;
                    }
                    current_col--; // Move the ball to the left
                }
            }
            
            // If the ball is not stuck, update the result
            if (current_col != -1) {
                result[col] = current_col;
            }
        }
        
        return result;
    }
};

Complexity Analysis:

• Time Complexity:
  • The outer loop iterates over all columns (O(n)), and for each column, we traverse each row (O(m)).
  • The overall time complexity is O(m * n).
• Space Complexity:
  • We use extra space for the result array, which has size n. Therefore, the space complexity is O(n).