Problem Statement

Given a circular arraynums, return the maximum possible sum of a non-empty subarray of nums.

Since the array is circular, the subarray can wrap around from the end of the array to the beginning.

A circular array means the end of the array connects to the beginning of the array. Formally, the next element of nums[i] is nums[(i + 1) % n] and the previous element of nums[i] is nums[(i - 1 + n) % n].

Examples

Example 1:

Input: nums = [1, -2, 3, -2]
Output: 3

Explanation:
The maximum subarray sum is [3], which gives a sum of 3.

Example 2:

Input: nums = [5, -3, 5]
Output: 10

Explanation:
The subarray can wrap around, so the maximum sum is [5, 5], which gives a sum of 10.

Example 3:

Input: nums = [-3, -2, -3]
Output: -2

Explanation:
The maximum subarray sum is [-2], which gives a sum of -2.

Different Approaches

1️⃣ Kadane's Algorithm

Intuition:

The problem can be broken into two main cases:

1. Non-circular subarray: This is the standard "Maximum Subarray Sum" problem, where we simply find the maximum sum of a contiguous subarray using Kadane's Algorithm.
2. Circular subarray: The maximum sum subarray may include both the end and the beginning of the array due to its circular nature. For this case, we need to calculate the total sum of the array and subtract the minimum subarray sum to get the maximum circular subarray sum.

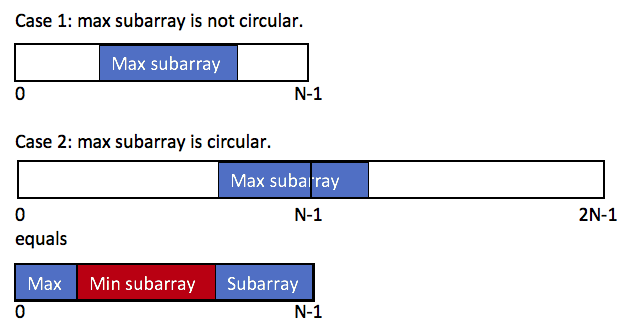
Why does subtracting the minimum subarray sum work?

• The intuition is that if the maximum sum subarray wraps around the end and the beginning of the array, it is equivalent to removing the minimum subarray (i.e., the subarray that contributes the least) from the middle of the array. The remaining part gives the maximum circular subarray sum.

Edge Case:

If all elements in the array are negative, the circular case would give an incorrect result (a total sum of zero). In this case, the result should simply be the maximum subarray sum (as taking any circular sum would involve removing the whole array, which is invalid).

Approach:

1. Calculate the total sum of the array.
2. Apply Kadane's Algorithm to find the maximum subarray sum for the non-circular case.
3. Apply Kadane's Algorithm to find the minimum subarray sum, since removing this subarray gives the circular maximum sum.
4. Compare the two results:
   • If the maximum subarray sum is from Kadane’s algorithm, the result is simply that value.
   • If the circular subarray sum (total sum minus the minimum subarray) is larger, return that.
5. Handle the edge case: If all numbers are negative, the circular subarray should not be considered, so return the non-circular result.

Code:

#include <iostream>
#include <vector>
#include <numeric>
#include <algorithm>

using namespace std;

// Function to calculate the maximum subarray sum using Kadane's Algorithm
int kadaneMaxSum(const vector<int>& nums) {
    int maxSoFar = nums[0];
    int currMax = nums[0];
    
    for (int i = 1; i < nums.size(); ++i) {
        currMax = max(nums[i], currMax + nums[i]);
        maxSoFar = max(maxSoFar, currMax);
    }
    
    return maxSoFar;
}

// Function to calculate the minimum subarray sum using Kadane's Algorithm
int kadaneMinSum(const vector<int>& nums) {
    int minSoFar = nums[0];
    int currMin = nums[0];
    
    for (int i = 1; i < nums.size(); ++i) {
        currMin = min(nums[i], currMin + nums[i]);
        minSoFar = min(minSoFar, currMin);
    }
    
    return minSoFar;
}

int maxSubarraySumCircular(vector<int>& nums) {
    // Step 1: Calculate the total sum of the array
    int totalSum = accumulate(nums.begin(), nums.end(), 0);
    
    // Step 2: Find the maximum subarray sum using Kadane's Algorithm
    int maxSubarraySum = kadaneMaxSum(nums);
    
    // Step 3: Find the minimum subarray sum using Kadane's Algorithm
    int minSubarraySum = kadaneMinSum(nums);
    
    // Step 4: Handle the edge case where all elements are negative
    if (maxSubarraySum < 0) {
        return maxSubarraySum; // If all numbers are negative, return the max subarray sum.
    }
    
    // Step 5: Return the maximum of the non-circular max and the circular max
    return max(maxSubarraySum, totalSum - minSubarraySum);
}

int main() {
    vector<int> nums1 = {1, -2, 3, -2};
    cout << "Maximum Sum Circular Subarray: " << maxSubarraySumCircular(nums1) << endl;
    
    vector<int> nums2 = {5, -3, 5};
    cout << "Maximum Sum Circular Subarray: " << maxSubarraySumCircular(nums2) << endl;
    
    vector<int> nums3 = {-3, -2, -3};
    cout << "Maximum Sum Circular Subarray: " << maxSubarraySumCircular(nums3) << endl;
    
    return 0;
}

Complexity Analysis:

• Time Complexity: O(n)
  • Kadane's algorithm for both maximum and minimum subarray sums takes O(n), where n is the size of the array.
  • Calculating the total sum of the array takes O(n).
  • Overall Time Complexity: O(n).
• Space Complexity: O(1)
  • We only use a few extra variables (e.g., totalSum, currMax, currMin), so the space complexity is O(1) (constant space).

Optimized Code:

    int maxSubarraySumCircular(vector<int>& A) {
        int total = 0, maxSum = A[0], curMax = 0, minSum = A[0], curMin = 0;
        for (int& a : A) {
            curMax = max(curMax + a, a);
            maxSum = max(maxSum, curMax);
            curMin = min(curMin + a, a);
            minSum = min(minSum, curMin);
            total += a;
        }
        return maxSum > 0 ? max(maxSum, total - minSum) : maxSum;
    }