Problem Statement

Given an array of elements, the task is to sort the array in non-decreasing (non-increasing) order. This means arranging the elements from the smallest to the largest (or vice versa).

Strategies

Bubble Sort is a comparison-based algorithm that works by repeatedly stepping through the list to be sorted, comparing each pair of adjacent items, and swapping them if they are in the wrong order. The pass through the list is repeated until no swaps are needed, which indicates that the list is sorted.

Algorithm

The basic steps of the Bubble Sort algorithm can be summarized as follows:

1. Start from the first element and compare it with the next element.
2. If the current element is greater than the next element, swap them.
3. Move to the next pair of elements and repeat steps 1 and 2 until the end of the array is reached.
4. Repeat the above steps for each element in the array until no more swaps are required.

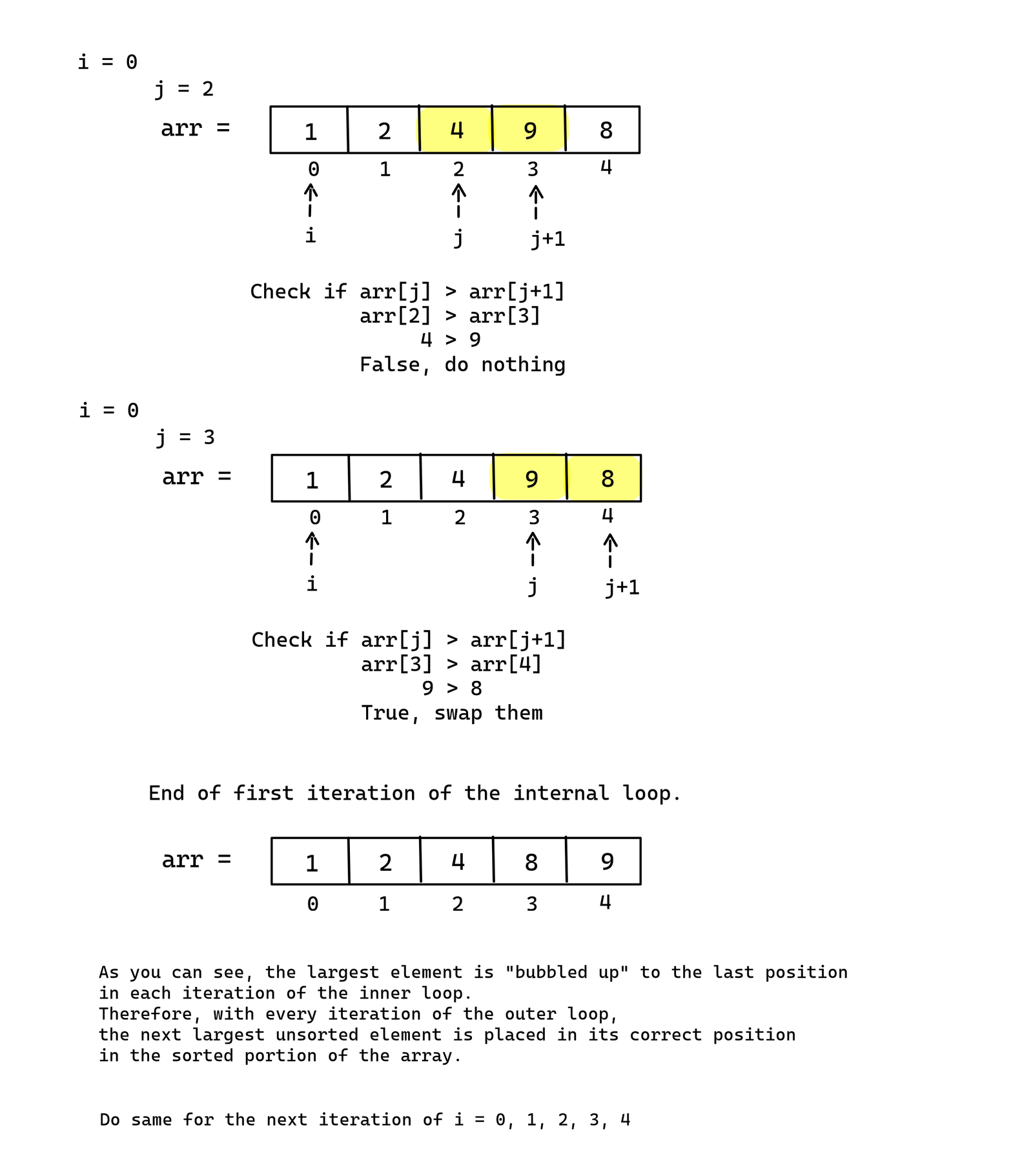
Code:

#include <iostream>

void bubbleSort(int arr[], int n) {
    for (int i = 0; i < n - 1; ++i) {
        for (int j = 0; j < n - i - 1; ++j) {
            if (arr[j] > arr[j + 1]) {
                // Swap arr[j] and arr[j + 1]
                int temp = arr[j];
                arr[j] = arr[j + 1];
                arr[j + 1] = temp;
            }
        }
    }
}

void printArray(int arr[], int n) {
    for (int i = 0; i < n; ++i) {
        std::cout << arr[i] << " ";
    }
    std::cout << std::endl;
}

int main() {
    int arr[] = {64, 34, 25, 12, 22, 11, 90};
    int n = sizeof(arr) / sizeof(arr[0]);
    std::cout << "Original array: ";
    printArray(arr, n);

    bubbleSort(arr, n);

    std::cout << "Sorted array: ";
    printArray(arr, n);

    return 0;
}

Output

0
1
4
9
23

Optimized Code:

The Bubble Sort algorithm makes multiple passes through the array even if the array is already sorted. We can add a flag to track whether any swaps were made during an iteration. If no swaps are made, it means the array is already sorted, and we can terminate early.

#include <iostream>

void optimizedBubbleSort(int arr[], int n) {
    bool swapped;
    for (int i = 0; i < n - 1; ++i) {
        swapped = false;
        // Last i elements are already sorted, so we don't need to traverse them
        for (int j = 0; j < n - i - 1; ++j) {
            if (arr[j] > arr[j + 1]) {
                // Swap arr[j] and arr[j + 1]
                std::swap(arr[j], arr[j + 1]);
                swapped = true;
            }
        }
        // If no two elements were swapped in the inner loop, the array is already sorted
        if (!swapped) {
            break;
        }
    }
}

void printArray(int arr[], int n) {
    for (int i = 0; i < n; ++i) {
        std::cout << arr[i] << " ";
    }
    std::cout << std::endl;
}

int main() {
    int arr[] = {64, 34, 25, 12, 22, 11, 90};
    int n = sizeof(arr) / sizeof(arr[0]);
    std::cout << "Original array: ";
    printArray(arr, n);

    optimizedBubbleSort(arr, n);

    std::cout << "Sorted array: ";
    printArray(arr, n);

    return 0;
}

Complexity Analysis

Time Complexity: O(n ^ 2)

• In the worst case scenario, when the array is in reverse order, this sorting algorithm performs poorly.
• The outer loop runs for (n - 1) iterations, where n is the number of elements in the array.
• In each iteration of the outer loop, the inner loop performs (n - i - 1) comparisons and swaps.
• Therefore, the worst-case time complexity is O(n ^ 2)

Space Complexity: O(1)

• It doesn't require any extra space other than the input array.