Problem Statement

Given a string of characters (with no spaces) as input, generate all possible permutations of the string by inserting spaces between its characters. The goal is to explore all ways of placing spaces such that each character can either be separated by a space or directly joined to the next character (means space cant be in beginning and ending of the string).

Constraints:

• The input string will contain only uppercase letters (A-Z) with no spaces.
• Output each unique permutation with spaces in any order.

Examples

Example 1:

Input: "ABC"
Output: "A B C"
        "A BC"
        "AB C"
        "ABC"
        
Explanation:
For the input string "ABC", we can generate the following permutations with spaces:
"A B C": Place a space between each pair of characters.
"A BC": Place a space only after the first character.
"AB C": Place a space only after the second character.
"ABC": Do not place any spaces.

Example 2:

Input: "AB"
Output: "A B"
        "AB"

Explanation:
For the input string "AB", we have two options:
"A B": Place a space between "A" and "B".
"AB": No space between "A" and "B".

Different Approaches

1️⃣ Recursion

Intuition:

Think of each character as having two options for the next character:

1. Either attach the character without a space.
2. Attach the character without a space.

For each character (after the first), we make two choices recursively until we reach the end of the string.

Approach:

1. Recursive Function: Start with the first character, then for each subsequent character:
   • Option 1: Attach it without a space.
   • Option 2: Attach it with a space.
   • Recursively repeat these choices until all characters have been processed.
2. Base Case: When we reach the last character, we add the current combination (permutation) to our result list.
3. Result Collection: All combinations are added to a result vector, which we print or return as needed.

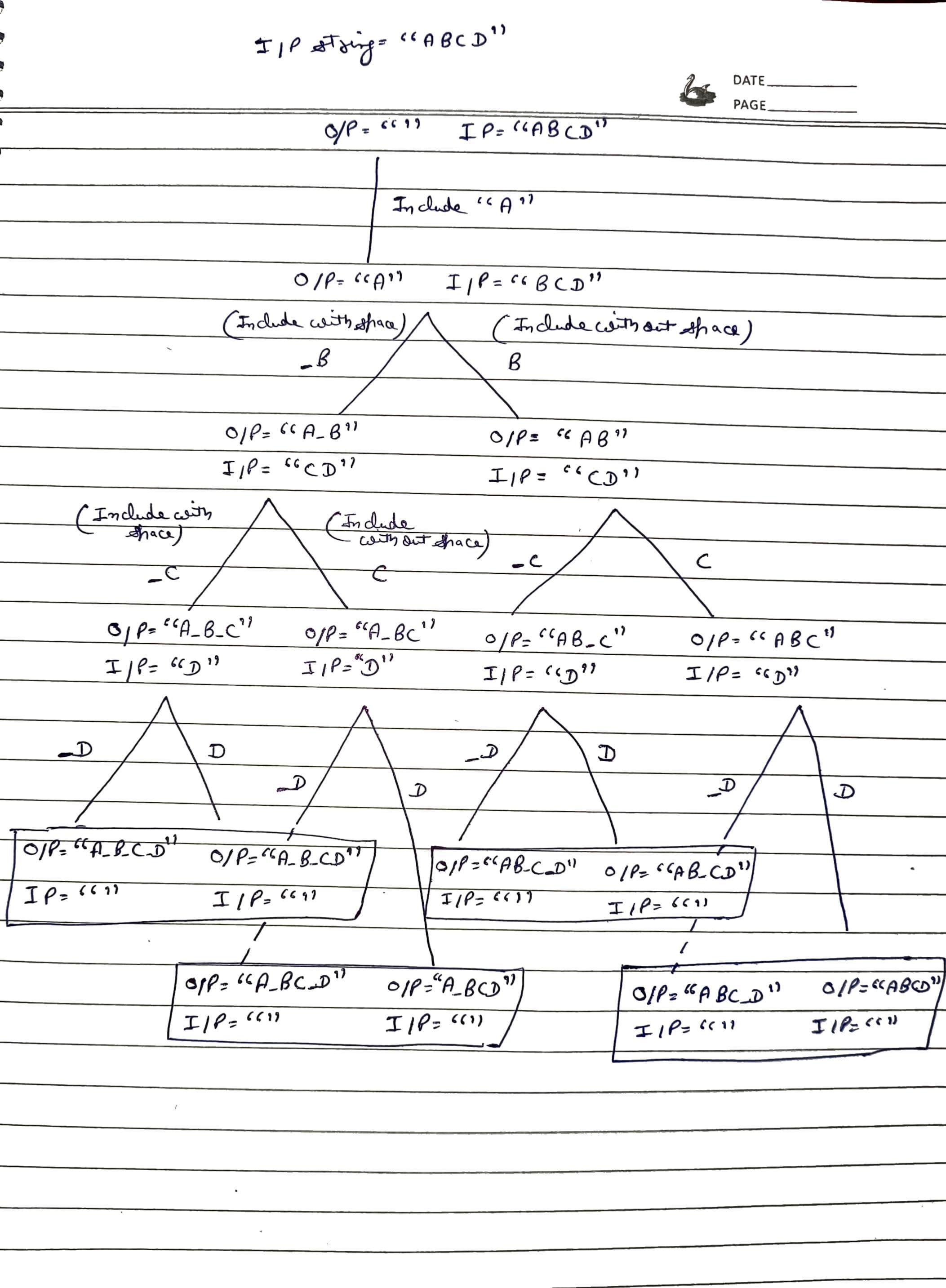
Recursive Tree Example

For the input “ABC”, the recursive choices form a tree structure where each level represents a decision (with or without space).

                        "A"
                      /      \
               "A B"         "AB"
               /    \         /     \
        "A B C"   "A BC"  "AB C"   "ABC"

Each path from the root to a leaf node represents a complete permutation:

• “A B C”
• “A BC”
• “AB C”
• “ABC”

Dry Run:

Let's do a dry run for the input “ABC”:

1. Start with "A".
2. For each character after the first:
   1. Attach "B":
      1. With space: current = "A B"
         • Attach "C" with and without space, yielding "A B C" and "A BC".
      2. Without space: current = "AB"
         • Attach "C" with and without space, yielding "AB C" and "ABC".

Code:

#include <iostream>
#include <vector>
#include <string>

using namespace std;

// Helper function to generate permutations with spaces
void generatePermutationsWithSpaces(string current, string remaining, vector<string>& results) {
    // Base case: if there are no remaining characters, add the current result
    if (remaining.empty()) {
        results.push_back(current);  // Add the current string to results
        return;
    }
    
    // Option 1: Add the next character without a space
    generatePermutationsWithSpaces(current + remaining[0], remaining.substr(1), results);
    
    // Option 2: Add the next character with a space
    generatePermutationsWithSpaces(current + " " + remaining[0], remaining.substr(1), results);
}

// Main function to initiate the recursive process
vector<string> permutationWithSpaces(string str) {
    vector<string> results;
    
    // Start recursion with the first character as the initial 'current' string
    if (!str.empty()) {
        generatePermutationsWithSpaces(string(1, str[0]), str.substr(1), results);
    }
    
    return results;
}

int main() {
    string str = "ABC";
    vector<string> results = permutationWithSpaces(str);
    
    // Print all permutations
    cout << "Permutations with spaces:" << endl;
    for (const string& perm : results) {
        cout << perm << endl;
    }
    
    return 0;
}

Complexity Analysis:

• Time Complexity: O(2^(n-1)), where n is the length of the string, as each character (except the first) has two options (with or without a space).
• Space Complexity: O(2^(n-1)), since we store all permutations in the results vector.